Normal Modes Analysis

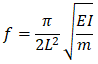
Learn more about START-PROF pipe stress analysis software

Modal analysis determines a piping system's natural frequencies and mode shapes under dynamic loading. Dynamic loads can amplify structural response beyond static load effects. Piping natural frequencies should avoid equipment operating frequencies to prevent resonance.

When piping natural frequencies approach equipment operating frequencies, resonance occurs, causing excessive vibration amplitudes. Modify system stiffness by adding supports, changing layout, or using rigid instead of flexible supports to shift natural frequencies away from excitation frequencies.

Increasing natural frequencies is generally preferable to decreasing them. START-PROF calculates natural frequencies and periods and provides animated mode shape visualization.

To perform modal analysis, enable the "dynamic" option in the operation mode editor for the relevant load case.

Mass Discretization

START-PROF uses a lumped mass model with uniformly distributed inertial forces. For accurate results, masses are properly discretized through automatic insertion of intermediate nodes with concentrated masses along pipe elements.

The maximum mass spacing is calculated based on the first natural frequency (f) of an equivalent simply supported beam:

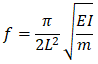
For two masses per span, the optimal element length (L) is:

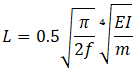
where:

f - Cut-off frequency from project settings (default: 33 Hz)

m - Mass per unit length (pipe, insulation, content, and additional weights)

E - Modulus of elasticity

I - Moment of inertia

When pipe or bend lengths exceed the optimal element length (L), additional lumped masses are inserted. Bends receive 3+ masses, tees 1+ masses, reducers 2 masses. Valves and flanges shorter than 0.5L receive 1 mass; longer elements receive 2 masses.

Nonlinear Effects Linearization

Dynamic analysis requires linear systems, so nonlinear elements are linearized:

• One-way restraints are ignored when inactive in operating mode; treated as double-acting when active
• Restraints with gaps are ignored when inactive; treated as double-acting when gaps are closed

• Friction effects are approximated with transverse spring stiffness:

where:

k - Friction coefficient for dynamic analysis (default: 40 1/mm or 1000 1/in)

Set k=0 to ignore friction; use large values (k=10000) for rigid restraint approximation

Rz - Restraint load from static analysis, μ - Friction factor

• Guide support friction is modeled with spring stiffness:

Rz - Vertical load, μz - Vertical friction factor, Ry - Horizontal load, μy - Horizontal friction factor

• Slip joint axial friction force F is modeled with spring stiffness:

• Torsion expansion joint and ball joint friction moments are modeled with spring stiffness:

• Rigid rod hanger and variable spring hanger rotation rod forces are modeled with spring stiffness:

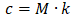
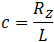
Rz - Vertical hanger load, L - Hanger length

Modal Analysis Theory

Undamped natural frequencies and mode shapes are obtained by solving the generalized eigenvalue problem:

where:

A - Flexibility matrix

V - Mode shape matrix

M - Mass matrix

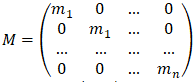
λ - Eigenvalue

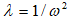
ω - Angular frequency (rad/s)

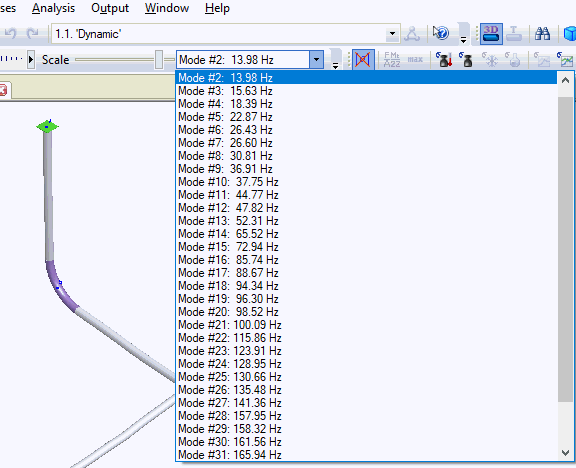
The model includes three mass degrees of freedom per node (rotational mass ignored). START-PROF's dynamic eigensolver calculates natural frequencies starting from the lowest until reaching the requested number of modes.

Results

Review natural frequencies and mode shapes in the Natural Frequencies and Periods table.

Angular Frequency (rad/s)

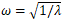
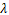- Eigenvalue from eigensolution

Frequency (Hz)

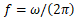
Period (s)

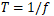
View animated mode shapes in the 3D Output View.