Variable and Constant Spring Selection in START-PROF

Learn about START-PROF pipe stress analysis software

Variable Spring Supports and Hangers

These supports use springs or spring assemblies to accommodate thermal expansion and control pipe stress through spring compression forces. Variable spring supports mount below the pipe (fig. 1a), while variable spring hangers suspend from above (fig. 1c).

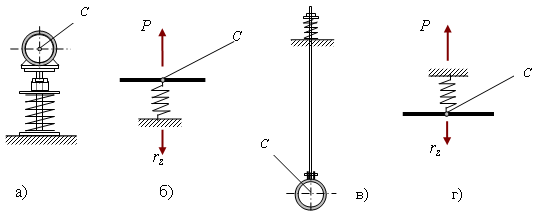
Fig. 1

A variable spring support can have one or more vertical spring assemblies, see fig. 2. Select the number of assemblies based on space constraints. Each assembly can stack multiple springs.

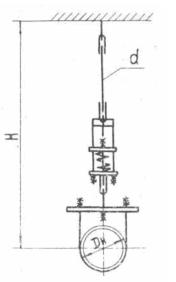
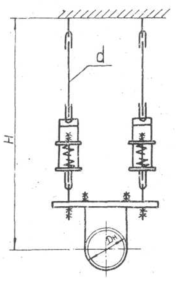
Fig. 2

Ignoring hanger tilt and friction effects, both configurations behave identically (fig. 1b and 1d). For analysis, we'll assume a single spring.

The support acts as a linear vertical spring restraint. The upward reaction force has two components

,

where

P_s - preload force from initial spring compression during installation (preload force),

r_z - spring reaction to pipe displacement at point C, equal to stiffness times displacement r_z = λ ·Δ.

The spring must remain compressed at all times. This allows variable spring supports to function as double-acting restraints. If analysis shows spring tension, the software displays a  warning message.

Preload Force P_s

Preload force  P_s is the concentrated force from compressing spring supports off-pipe. P_s is determined by the  spring support pre-tensioning method.

The operating and cold loads on the spring (R_op and R_cold) vary with operating conditions. But the preload value remains constant. This lets you reuse springs while modifying the pipe design. For different analysis cases like Equipment Nozzle Load Check or transportation analysis, convert springs to custom restraints.

Spring Assembly Structure and Variable Spring Support Flexibility

Springs fall into two classes: Class 1 allows 70mm maximum travel (operating deflection) and Class 2 allows 140mm maximum travel. "1+2+2" denotes one Class 1 spring and two Class 2 springs in series.

In this example, the assembly structure is 1+2+2=5, with total allowable travel of 5*70 = 350mm. Spring codes follow  industry standards specified in Project Settings.

Flexibility describes the elastic behavior of a spring support or hanger with one or more spring assemblies. Total travel  λ depends on the number of springs and their individual flexibility. In the example above, total flexibility is

l= l₇₀ + l₁₄₀ + l₁₄₀

Class 2 spring flexibility (l₁₄₀) is twice that of Class 1 springs (l₇₀). l₁₄₀ = 2·l₇₀. Thus, total flexibility equals:

l=5·l₇₀

Stiffness K is the inverse of flexibility

K=1/l

Automatic Variable Spring Hanger Selection

Ideally, the pipe should respond to thermal expansion like a weightless spring. Spring support compression is set to counterbalance the heated pipe's weight. At each support point, spring reactions should produce zero vertical displacement from weight loads [1].

Proper spring selection requires:

1. Load variation between operating and cold conditions must not exceed 25%

Variation=(R_op-R_cold)/R_op*100%≤25%

Achieve this by selecting appropriate spring stiffness λ. Lower stiffness makes this condition easier to satisfy. With large visible displacement  Δ_vis, you may need to replace the spring with a constant support. Two types of visible displacement exist:

Inst-Ope: Δ_vis = Δ_inst - Δ_op = (R_inst - R_op)·l·n

Ope-Cold: Δ_vis = Δ_op - Δ_cold = (R_op - R_cold)·l·n

2. Spring allowable load must exceed both R_op and R_cold.

n - number of spring assemblies

For cold mode spring selection, swap cold and operating loads in the formulas.

START-PROF selects springs in two steps:

Step 1: Replace all springs with rigid unidirectional supports. Apply weight loads only. Determine maximum operating spring loads R_max=R_op/n. Select springs with allowable load exceeding R_max from the database.

Step 2: Add stiffness from selected springs. Apply thermal and displacement loads only. Determine operating displacements Δ_op. Calculate maximum spring load R_max=R_op/n if Δ_op≤0 and R_max=(1+Variation/100%)·R_op/n if Δ_op>0. Calculate minimum stiffness λ = (Variation/100%)·R_op/(Δ_op·n). Select springs with allowable load exceeding R_max and stiffness less than l.

Variation=(R_op-R_cold)/R_op*100% - load variation between cold and operating conditions.

Step 2 repeats until spring selection stabilizes.

See the table below:

START-PROF can select:

1. Spring support flexibility  λ  and corresponding spring assembly properties: spring types, quantity, and number of assemblies. The software selects assembly composition when flexibility (stiffness) in spring support or spring hanger properties is set to 0. START-PROF calculates the minimum number of assemblies needed to meet allowable load requirements. Springs are automatically selected with sufficient capacity for forces  R_op and R_cold.
2. Spring support or hanger reaction forces  R_op, R_cold, R_assembly, P_s. Automatic force selection occurs when reaction forces in spring support or spring hanger properties are set to 0. Non-zero values let you manually control pipe forces and stresses.

Automatic spring support selection follows  [1]. For manual control of forces and stresses, input reaction forces and flexibility directly. Manual adjustment can yield more economical results than automatic selection per  [1]. Manual adjustment of spring support forces is often necessary to reduce equipment nozzle loads. Use the transfer function to copy automatically calculated spring properties to input data for manual editing.

Spring selection can use two conditions (set in Project Settings):

1. Zero displacement from weight loads in the operating condition (operating weight balance). Use with two-step compression or pre-tensioning.
2. Zero displacement from weight loads in the cold condition (cold weight balance). Use with single-step compression (lift-off method).

For high-temperature pipelines (Т_op>350⁰), select and adjust springs for operating conditions (using two-step compression or pre-tensioning). For low-temperature pipelines (Т_op≤350⁰), use single-step installation, and select springs for cold conditions.

Note: START-PROF selects springs per  [1] assuming linear behavior (no friction, pendulum effects, etc.), then analyzes the pipe with nonlinear effects. Thus, the calculated load variation may exceed the selection input value. In this case, input a lower variation and re-analyze.

The table below shows input and calculated spring support loads based on the selection condition.

Allowable Load Requirements

Spring support loads in all conditions must not exceed the allowable load R_max with safety factor  m [1].

m∙R_op ≤ R_max
m∙R_cold ≤ R_max

m - safety factor set in  spring properties.

The software automatically selects springs so that loads  R_op and R_cold do not exceed the allowable load R_max. For manual input forces, the software checks and displays messages. If springs are modeled as custom restraints, you must manually verify allowable load requirements.

For  support pre-tensioning, meet this condition:

m∙P_s ≤ R_max

The software does not check this condition automatically!

For two-step compression or lift-off method, no "pre-tensioning" state exists, so no allowable load check is needed.

Spring Support and Hanger Installation Methods

Three methods exist  [1], [2]:

1. Pre-tensioning

2. Lift-off method

3. Two-step compression

Support Pre-tensioning

Use for spring selection in both  cold and operating conditions.

1. Free spring height is H_free, with zero compression force R_free=0.

2. Pre-compress the spring off-pipe (e.g., on the floor) using a jack. Compress to the preload force P_s. The corresponding height is H_s. Lock the compression with temporary ties welded to the spring housing. Install the spring on the pipe resting on temporary rigid supports, and remove all gaps (by adjusting rod length, adding shims, etc.). Support load is R_s=0, spring compression force is P_s and spring height is H_s. This is the installation state before spring adjustment.

3. Cut the temporary ties. The pipe immediately displaces by Δ_assembly, moving to the installation state after spring adjustment. Now both the spring support and the pipe act as springs. Installation support load is  R_assembly, and spring height is H_assembly.

R_assembly= P_s - Δ_assembly/λ
H_assembly = H_s + Δ_assembly

4. After filling and heating the pipe to operating temperature, displacement from the "original" state is Δ_op, support load is  R_op and height is H_op.

R_op= P_s - Δ_op/λ
H_op = H_s + Δ_op

5. After cooling and depressurizing, displacement from the "original" state is  Δ_cold, support load is R_cold, and spring height is H_cold.

R_cold= P_s - Δ_cold/λ
H_cold = H_s + Δ_cold

Negative signs occur because START-PROF uses consistent positive directions for concentrated forces and linear displacements.

R_op and R_cold - spring support reactions in operating and cold conditions. Knowing these forces and support flexibility l, calculate visible pipe displacement between cold and operating conditions:

Δ_vis = |Δ_op - Δ_cold| = |H_op - H_cold| = | λ (R_op - R_cold)|

Single-Step Compression ("lift-off method")

Use for spring selection in  cold condition.

Gradually lift the pipe from temporary rigid supports using spring compression. The resulting spring compression creates reactions that balance the pipe weight.

For low-temperature pipes, spring thermal displacement is small compared to high-temperature pipes, so further compression is unnecessary.

No need to select spring height  H_assembly values. Stop compression once the pipe lifts off the temporary supports. This method eliminates height  H_assembly analysis inaccuracies.

For this analysis type, select springs for cold conditions. Actual installation forces  R_assembly and displacements H_assembly should theoretically match design values from the zero weight displacement condition in  cold conditions (cold weight balance). Differences may occur due to modeling inaccuracies (model vs. actual structure differences).

Two-Step Compression

Use for spring selection in operating condition.

Lift the pipe from temporary rigid supports using spring compression. Remove the temporary supports and continue compression until reaching design height H_assembly and force R_assembly.

In this case, installation springs are "over-compressed". After heating, thermal displacement occurs, operating force becomes R_op, and height becomes  H_op. Pipe weight in operating condition is balanced, since spring selection ensures zero displacement from weight loads in operating condition (operating weight balance).

References

1. RTM 24.038.12-72 Variable spring hanger selection for nuclear and power plant piping. Ministry of Heavy, Power and Transport Engineering. Moscow 1973

2. D. Kostovetsky, B. Tokarski. On spring support preloading. CKTI Proceedings. Pipeline Design and Calculation for Power Plants. Issue 67, Saint Petersburg, 1966

3. V. Nakhalov. Spring Support Adjustment for Power Plants, Moscow 1975