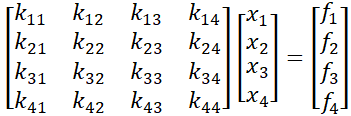
Поверочный расчет проводится после выбора основных размеров трубопровода и расстановки опор. При этом толщина стенок труб и фасонных деталей трубопровода должна соответствовать требованиям норм.
При выполнении расчета трубопровод рассматривается как упругая стержневая система. Учитывается повышенная податливость на изгиб отводов, секторных колен, косых стыков и ответвлений тройников, а также деформация сдвига для труб. Трубопровод разбивается на прямолинейные и криволинейные участки. Точки сопряжения участков называются узлами. Узлы ставятся в следующих случаях:
в местах присоединения к сосудам, аппаратам, резервуарам, коллекторам и т.д.;
в местах установки опор;
в точках изменения направления и разветвления осевой линии трубопровода;
в точках изменения характеристик трубы или грунта (давление, толщина стенки и т.д.).
При расчете учитываются нелинейные эффекты, обусловленные:
трением в опорах скольжения
отклонением тяг подвесок от вертикального положения
односторонними связями, связями с зазорами
взаимодействием трубопровода с грунтом на участках бесканальной прокладки
При необходимости по программной системе осуществляется:
автоматический подбор пружин упругих опор и расчет их затяжки
оценка прочности и несущей способности трубопровода и соединительных деталей по различным нормам
Расчет программой СТАРТ-ПРОФ выполняется по следующей схеме
Логическая проверка всех исходных данных на наличие ошибок и предупреждений. В случае их обнаружения выдаются сообщения об ошибках или предупреждениях.
Проверка всех деталей трубопровода на давление. Если хотя бы одна из деталей трубопровода не проходит по расчетному давления или по давлению испытаний, выдается ошибка и расчет прекращается. Это правило применяется для всех Российских нормативных документов
Подбор пружин
Серия расчетов трубопровода по методам строительной механики с учетом различных нелинейных эффектов на различные редактор режимов работы
Вычисление напряжений и проверка условий прочности по нормам
Выдача примечаний о проблемах в результатах расчета
Результаты расчета доступны
В виде примечаний в окне "ошибки и предупреждения"
При расчете трубопроводов в СТАРТ-ПРОФ используется смешанный метод строительной механики стержневых систем [1], [7]. Трубопровод рассматривается в качестве стержневой системы, состоящей из прямых и кривых стержней. К прямым стержням относятся трубы и трубопроводная арматура, к кривым - отводы и гнутые трубы. В программе учитывается повышенная гибкость отводов и гнутых труб за счет овализации их сечения при изгибе (эффект Кармана).
За неизвестные усилия принимаются реакции отброшенных связей в консольной основной системе, а за неизвестные перемещения - перемещения по направлению отсутствующих в узлах связей, которые в основной системы были заданы жесткими. В результате формируется линейная система алгебраических уравнений, решение которой дает неизвестные усилия в отброшенных связях и перемещения по направлению дополнительно наложенных связей.
При программа учитывает нелинейные эффекты, вызванные:
трением в опорах скольжения;
отклонением тяг подвесок от вертикального положения;
односторонними связями;
взаимодействием трубопровода с грунтом;
Наличие нелинейностей, обусловленных работой односторонних связей, а также опор с трением, учитывается с помощью итерационной процедуры, в которой на каждом шаге решается линейная система уравнений.
При наличии опор с трением используются условия:
суммарная реакция фрикционных связей, моделирующих опору с трением равна силе трения покоя или движения с погрешностью 5%;
перемещение по направлению силы трения равно нулю (сила трения покоя), либо направлена в обратную сторону (сила трения движения).
Программа позволяет производить автоматический подбор пружин пружинных опор и расчет их затяжки, реализованный на основе правил, опубликованных в литературе [4,5].
При расчете участков трубопровода, защемленных в грунте, расчетная модель грунта представляется зависимостью сопротивления грунта от перемещения, причем эта зависимость различна и определяется направлением перемещения трубопровода относительно поверхности земли. Зависимость сопротивления грунта от перемещения нелинейная. Принятая в программной системе расчетная модель грунта основана на результатах экспериментальных и теоретических исследований [2,3].
Грунт является непрерывным основанием, которое моделируется дискретно расставленными по длине трубопровода нелинейно-упругими опорами, жесткость которых зависит от величины и направления перемещений. В СТАРТ-ПРОФ реализован алгоритм, предложенный А.Б Айнбиндером. Каждая нелинейно-упругая опора состоит из трех связей: вертикальной, горизонтальной (поперек оси трубы) и продольной (вдоль оси трубы). Итерационная процедура заканчивается, когда на очередном шаге перемещения по направлению связей перестают меняться. Расстояния между опорами определяются автоматически.
Классические программы по расчету конструкций методом конечных элементов используют метод перемещений. Решается система уравнений в матричном виде K*X=F [7].
K - матрица жесткости
X - вектор перемещений (неизвестные)
F - вектор нагруок
Для системы с 4 степенями свободы уравнения в матричном виде будут выглядеть так:
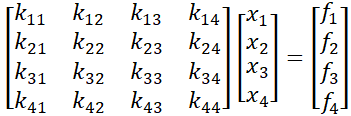
Главный недостаток этого метода - большое число степеней свободы, а соответственно большое потребление памяти и низкая скорость расчета. А достоинство - это то, что задачи легко формализуются при реализации в программах для компьютера.
В методе сил решается система уравнений в матричном виде A*F=D [7].
A - матрица податливости
F - вектор нагрузок (неизвестные)
D - вектор перемещений
Для системы с 4 степенями свободы уравнения в матричном виде будут выглядеть так:
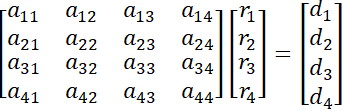
Главное достоинство этого метода - малое количество степеней свободы, соответственно, низкое потребление памяти и высокая скорость расчета. Главный недостаток - сложная реализация в программах для компьютера.
В программе СТАРТ-ПРОФ реализован смешанный метод расчета. Комбинация метода сил и метода перемещений. Причем, в большинстве трубопроводных систем количество степеней свободы метода сил оказывается существенно больше степеней свободы метода перемещений. Неизвестными являются как нагрузки на опоры, так и перемещений в "разрезах" и компенсаторах.
В матричном виде метод выглядит так:
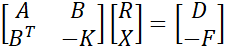
A - матрица податливости (перемещения от единичных сил, приложенных по направлению неизвестных сил r)
K - матрица жесткости (реакции, вызванные единичными смещениями по направлениях неизвестных перемещений)
B - матрица перемещений от единичных сил, приложенных по направлениях неизвестных перемещений x
R - вектор неизвестных сил
X - вектор неизвестных перемещений
D - вектор приложенных перемещений
F - вектор приложенных сил
Например, мы имеем раму с 4 узлами (a) с мертвыми опорами в узлах 1 и 4, шарниром в узле 2 и силой, приложенной в узле 3
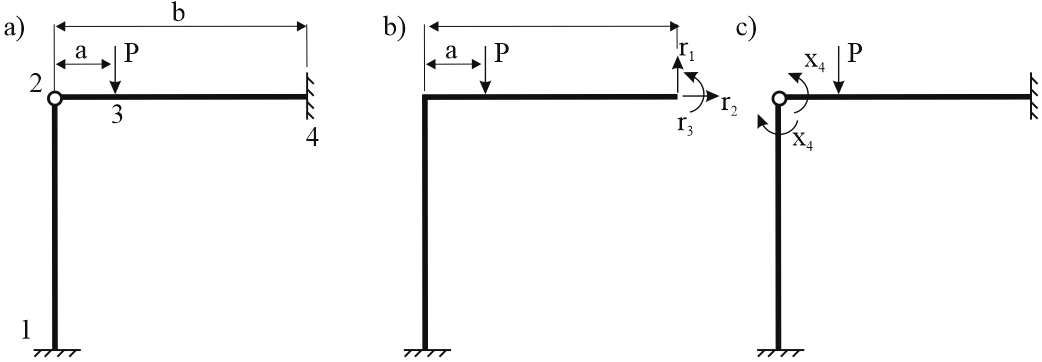
a - модель рамы, b - основная система для метода сил, c - основная система для метода перемещений
Основная система для метода сил (b) получана путем отбрасывания мертвой опоры 4 и заменой на 3 неизвестных силы r1, r2, r2. Узел 2 считается жестким, шарнира нет.
Основная система метода перемещений получена путем приложения неизвестных перемещений x4 в шарнире 2 (c).
Система уравнений в матричном виде будет выглядеть следующим образом:
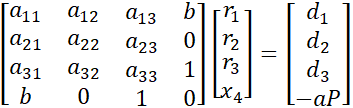
Уравнение в последнем ряду означает, что сумма моментов сил в шарнире должна быть равна нулю:
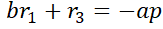
Этот метод был выбран авторами СТАРТ-ПРОФ [1] в 1965 году, поскольку является самым экономичным по использованию памяти и самым быстрым по скорости при реализации на компьютере для типичных трубопроводных систем, которые имеют разветвленную древо-подобную структуру. В то время это имело огромное значение. На современных машинах этот метод позволяет решать достаточно большие нелинейные задачи в несколько раз быстрее, чем классический метод перемещений, который выбирает большинство разработчиков программ из-за удобства программирования.
Например, мы имеем следующую трубопроводную систему:
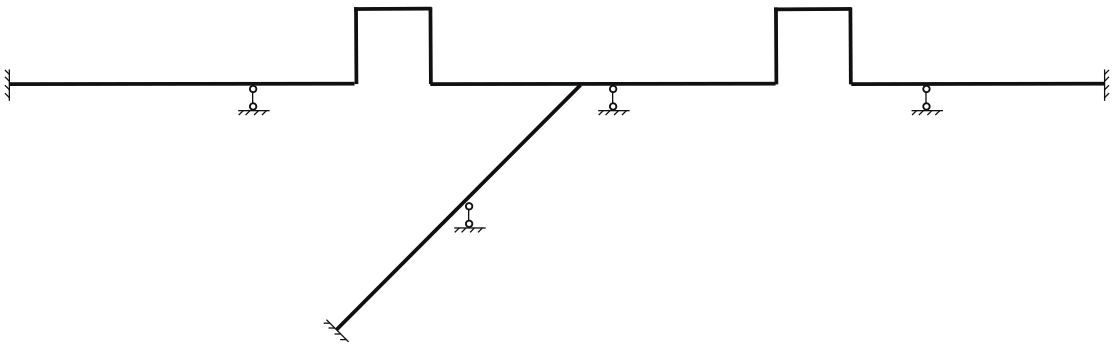
При решении методом перемещений данная система будет иметь как минимум 78 степеней свободы (неизвестных). Матрица K будет 78x78.
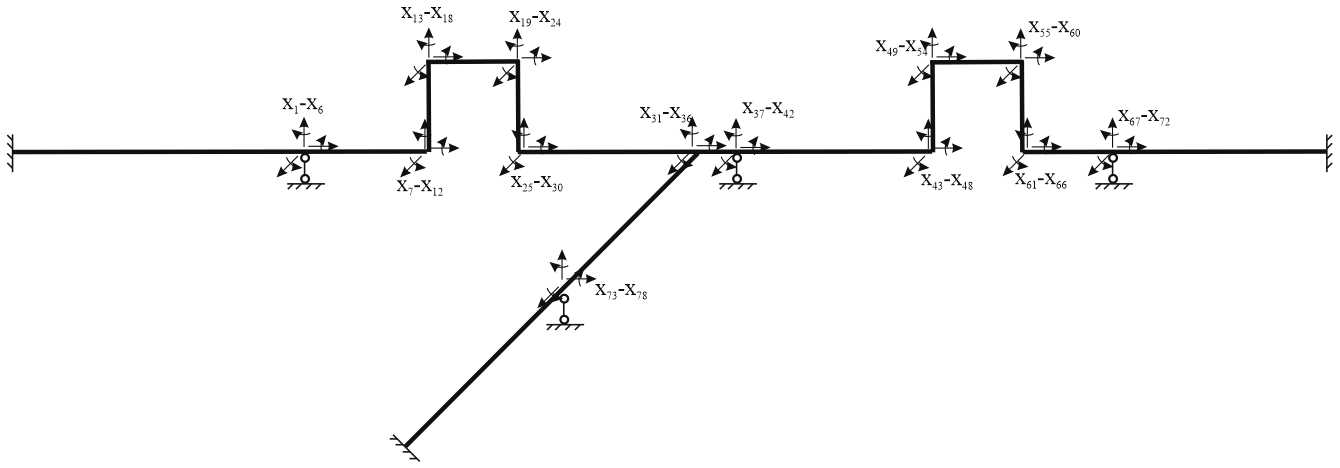
В СТАРТ-ПРОФ, при использовании смешанного метода расчета эта система будет иметь всего лишь 24 степени свободы. Матрица будет 24x24.
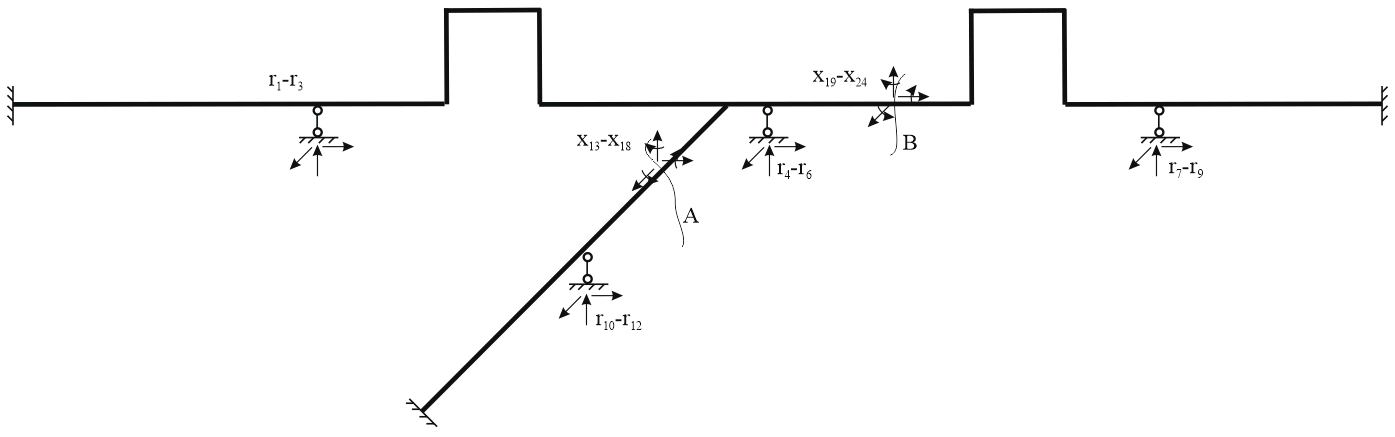
Для того, чтобы превратить данную систему в три консольных системы ("консоли"), которые легко поддаются формализации при расчете методом сил, добавляются специальные "разрезы" A и B. В каждом таком "разрезе" добавляются по 6 степеней свободы метода перемещений x.
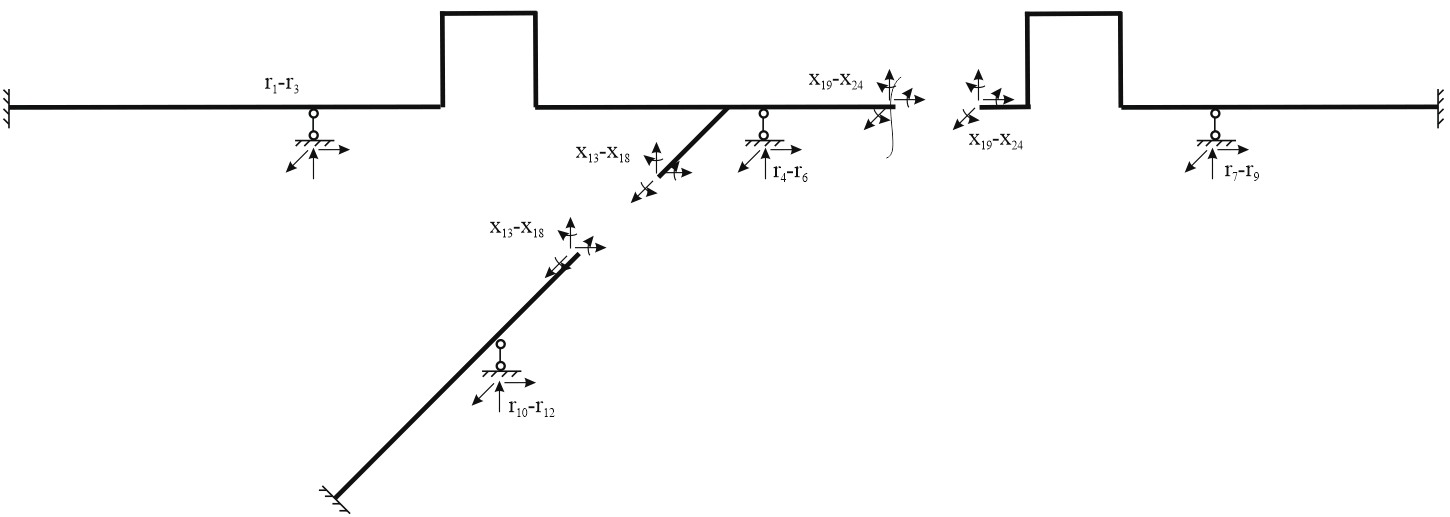
В методе перемещений, используемом в большинстве МКЭ программ неизвестными решения системы линейных уравнений являются перемещения x. Граничными условиями также являются перемещения (нулевые перемещения в точках установки опор). Поэтому, даже когда мы решаем нелинейные задачи с заданной точностью, перемещения на опорах всегда являются точными, т.к. они заданы изначально. Например, на скользящих опорах мы всегда будем получать вертикальное перемещение 0, если она работает.
В методе сил неизвестными являются нагрузки на опоры, поэтому когда мы решаем нелинейную задачу с заданной точностью, эти нагрузки будут получены также с некоторой погрешностью. При вычислении перемещений в "консолях" с использованием этих нагрузок могут получиться не нулевые перемещения в жестких опорах (то есть тоже, с некоторой погрешностью). Например, на скользящих опорах мы можем получить перемещение -0.5 мм для очень длинных консолей. Обычно это вызывает вопросы у специалистов, не знакомых со смешанным методом и привыкших к методу перемещений. На самом деле это не является ошибкой, а является особенностью метода. Так же как и в методе перемещений мы получаем реакции в опорах с некоторой погрешностью. Просто ее не так легко зметить, как перемещения на опорах. Обычно это не требует какой-либо реакции со стороны пользователя.
Но если есть желание получить перемещения еще более точно, то можно воспользоваться специальным объектом - Маркером (М). Маркер добавляет 6 лишних неизвестных метода перемещеений и разрывает каждую консоль, в которую он установлен на две части. Это приводит к существенному повышению точности вычисления перемещений после расчета.

1. Магалиф В.Я., Якобсон Л.С. Расчеты трубопроводов на вычислительных машинах. М. Энергия, 1969.
2. Айнбиндер А.Б., Камерштейн А.Г. Расчет магистральных трубопроводов на прочность и устойчивость. М. “Недра”.1982 г.
3. Скоморовский Я.З., Айнбиндер А.Б., Продольные перемещения подземных трубопроводов с учетом физической нелинейности сопротивления грунта при сдвиге. Вопросы прочности трубопроводов 1975 г, (Труды ВНИИСТ, вып. 25).
4. Выбор упругих опор для трубопроводов тепловых и атомных электростанций. РТМ 24.038.12-72, Министерство тяжелого, энергетического и транспортного машиностроения. 1973.
5. ОСТ 108.764.01-80. Пружины винтовые цилиндрические для подвесок трубопроводов ТЭС и АЭС. Конструкция, размеры и технические требования, НПО ЦКТИ. 1981.
6. Программа расчета прочности и жесткости трубопроводов (СТАРТ-ПРОФ), ЦНИИПроект, 1986, (Межотраслевой фонд алгоритмов и программ автоматизированных систем в строительстве; выпуск 1-225-1).
7. А.В.Дарков, Н.Н.Шапошников Строительная механика