Функция доступна только при наличии опции "СТАРТ-грунт".
Учет взаимодействия трубы с окружающим грунтом производится согласно методике, разработанной А.Б. Айнбиндером для СТАРТ-ПРОФ (в то время программа называлась "СТ-01"). Методика основана на результатах экспериментальных и теоретических исследований во ВНИИСТе и других организациях и является уточненным вариантом методики, описанной в [1] и [6].
Модель грунта, реализованная в СТАРТ-ПРОФ учитывает:
Различные нелинейные эмпирические зависимости сопротивления грунта перемещениям трубы в вертикальном, горизонтальном и продольном направлении
Влияние жесткости пенополиуретановой изоляции
Влияние жесткости амортизирующих подушек в горизонтальной плоскости
Изменение свойств грунта, находящегося во взвешенном состоянии на обводненных участках
Вертикальные выталкивающие силы, действующие на обводненных участках
Изменение сил сопротивления грунта на вертикальных участках и участках с произвольным углом наклона
Учащение расстановки грунтовых опор вблизи точек с большими поперечными и продольными перемещениями
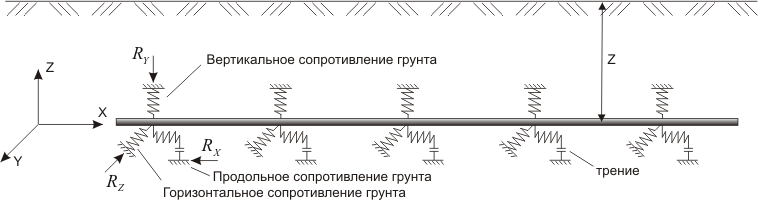
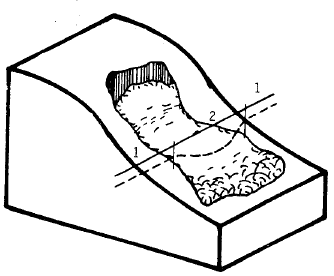
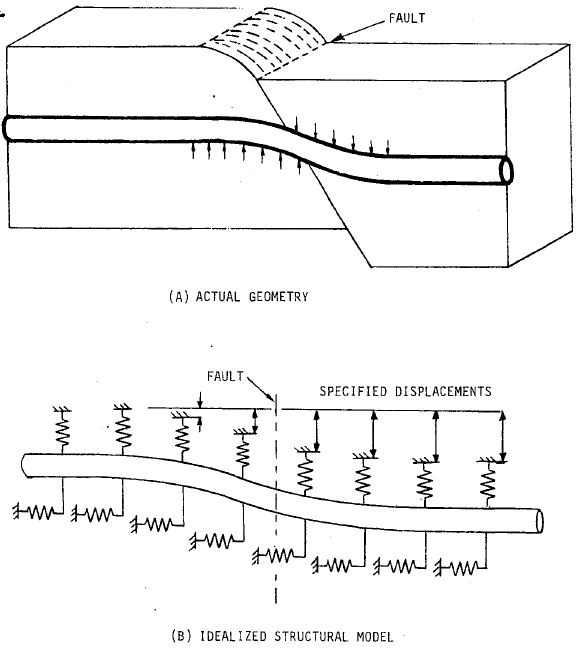
В СТАРТ-ПРОФ используется балочная расчетная модель трубопровода, при этом взаимодействие трубопровода с окружающим грунтом моделируется продольными и поперечными упругими опорами (билинейными пружинами), расставленными с определенным шагом (рис. 1).
Рис. 1. Модель взаимодействия трубопровода с окружающим грунтом
Расстановка пружин осуществляется программой СТАРТ-ПРОФ автоматически. При этом вблизи узлов учащения расстановки опор выделяется три зоны (рис. 2):
Зона #1: Зона изгиба длиной Lb. В этой зоне устанавливается четыре грунтовые опоры на равном расстоянии
Зона #2: Зона скольжения длиной La. В этой зоне устанавливается четыре грунтовых опоры на расстоянии, увеличивающемся в геометрической прогрессии от зоны #1 к зоне #3
Зона #3: Зона защемления. В этой зоне грунтовые опоры расставляются с шагом 100D, где D - наружный диаметр трубопровода
Пружины, моделирующие взаимодействие с грунтов всегда расставляются одинаково для всех режимов работы. При этом длины La и Lb вычисляются по данным самого первого режима ПДН.
Учащение расстановки опор производится автоматически в узлах, вблизи которых возможны большие поперечные или большие осевые перемещения, а именно в узлах:
с Т-образным соединением
с отводом любого вида
с поворотом оси трассы
с компенсатором любого вида
с монтажной растяжкой
с линейным смещением в узле
со свободным концом
со скользящей опорой с заданным смещением
с направляющей опорой с заданным смещением
с мертвой опорой с заданным смещением
с нестандартным креплением с заданным смещением
с арматурой
на границе с надземным участком
на границе между участками с просадкой и без просадки
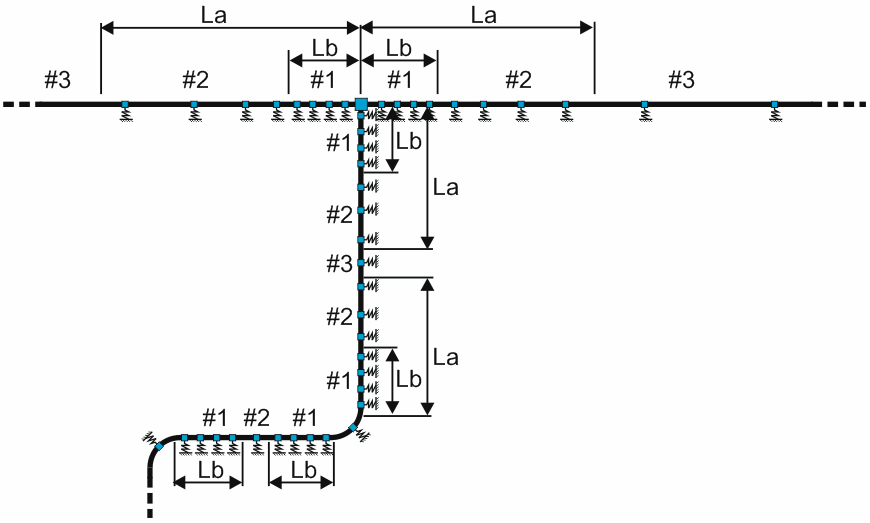
Рис. 2. Расстановка упругих опор, моделирующих взаимодействие с грунтом
В зоне изгиба #1 происходят большие изгибные деформации и поперечные перемещения трубопровода (рис. 3). Для повышения точности расчетной модели программа устанавливает четыре грунтовые опоры.
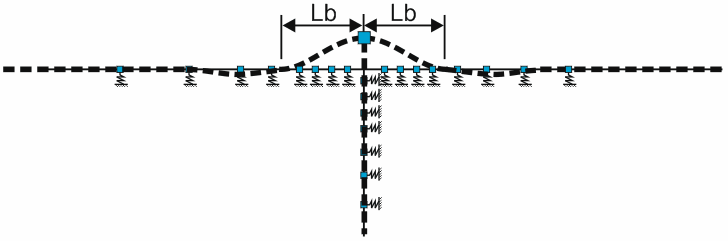
Рис. 3. Зона изгиба #1
В зоне скольжения #2 происходят большие продольные деформации и перемещения трубопровода (рис. 4). Для повышения точности расчетной модели программа устанавливает четыре грунтовых опоры с шагом, увеличивающимся в геометрической прогрессии от зоны #1 к зоне #3.
Смотрите подробнее Защемленный и не защемленный участок.
Рис. 4. Зона скольжения #2
В зоне защемления не происходит ни изгиба, ни продольных перемещений. Поэтому грунтовые опоры расставляются с очень большим шагом, принятым в программе равным 100D
Смотрите подробнее Защемленный и не защемленный участок.
Жесткости грунтовых опор вычисляются как общая жесткость цепи из нескольких пружин (рис. 5).
Жесткость K1 представляет собой нелинейную функцию, зависящую от относительной деформации подушек. Вычисляется также на основе эмпирических зависимостей по результатам экспериментов [3]. Наличие или отсутствие компенсирующих подушек задается в свойствах участков бесканальной прокладки.
Жесткость K2 представляет собой нелинейную функцию, зависящую от относительной деформации слоя ППУ и вычисляется на основе эмпирических зависимостей, полученных по результатам экспериментов [3]. Для вычисления жесткости ППУ в свойствах участков бесканальной прокладки должен быть задан диаметр кожуха изоляции.
Жесткость пружин, моделирующих грунт различна в зависимости от направления (рис. 5). Существует три типа пружин, моделирующих грунт:
пружины, препятствующие боковым перемещениям трубы в горизонтальной плоскости (горизонтальное сопротивление грунта) K3
пружины, препятствующие вертикальным перемещениям трубы (вертикальное сопротивление грунта) K4
пружины, препятствующие продольным перемещениям трубы (продольное сопротивление грунта) K5
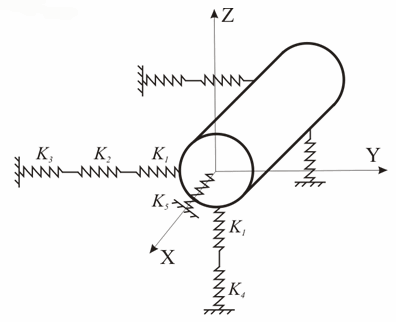
Рис. 5. Учет влияния жесткости слоя ППУ-изоляции и амортизирующих подушек
Общий вид графиков функций зависимости реакции в пружинах от перемещений представлены на рис. 4. Значения этих функций вычисляются на основе данных, заданных в свойствах участков бесканальной прокладки, а также данных о свойствах грунта засыпки и основания, которые задаются в базе данных по грунтам.
Пружины, препятствующие боковым перемещениям трубы в горизонтальной плоскости K3, имеют зависимость реакции от перемещения, показанную на рис рис. 6,а. Для вертикальных и продольных пружин зависимость показана соответственно на рис. 6,б и рис. 6,в.
После запуска расчета СТАРТ-ПРОФ автоматически выполняет серию последовательных приближений (расчетов) и на каждом шаге уточняются значения жесткостей всех пружин K1, K2, K3, K4 и K5. При достижении определенной точности расчет заканчивается.
Рис. 6. Графики функций нелинейных зависимостей сопротивления грунта от перемещений в различных направлениях относительно оси трубы
Глубина заложения, высота воды и просадка могут меняться по длине трубы, для этого задаются значения этих величин в начале Zн, Hвн, Δн и в конце Zк, Hвк, Δк каждого участка (рис. 6). Глубина заложения, высота воды и просадка фактически задаются в узлах, а не в участках. Поэтому указанные величины для одного и того же узла на двух смежных участках должны быть равны. Например, при изменении глубины заложения в узле для одного участка, глубина автоматически изменится в данном узле для другого примыкающего к нему участка.
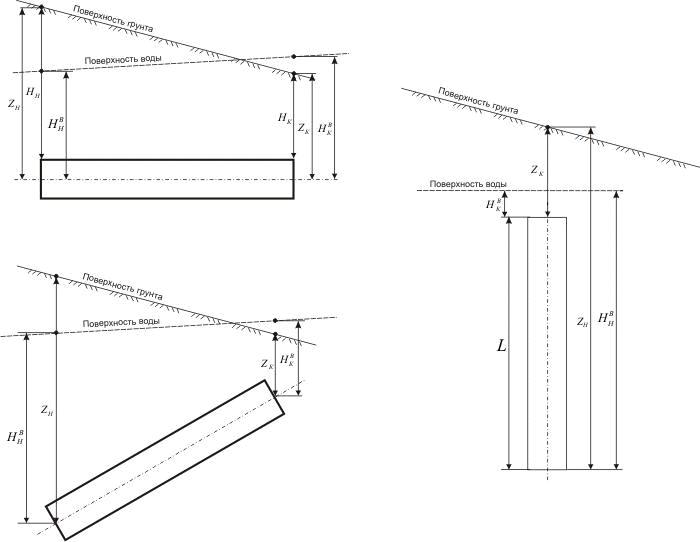
Рис. 6. Глубина заложения, высота воды по длине участка
В расчетной схеме при вычислении свойств каждой тройки пружин K3, K4 и K5 используется различная глубина заложения Zi и высота воды Hвi, полученная линейной интерполяцией заданных глубин в начале и в конце участка Zн и Zк (рис. 7). Выталкивающие силы воды также вычисляются в зависимости от высоты воды Hвi в каждой точке. Величина просадки для каждой пружины Δi вычисляется аналогичным образом, с помощью линейной интерполяции Δн, Δк.
Свойства пружин K3, K4 и K5 также пересчитываются в зависимости от угла наклона участка к горизонтальной плоскости (от 0 до 90 градусов), для вертикальных участков K4=K3.
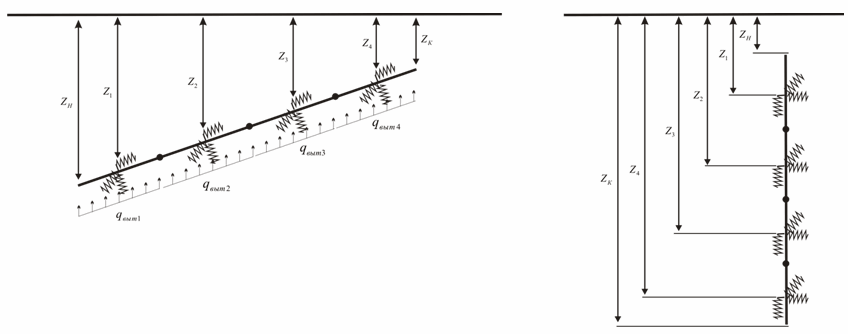
Рис. 7. Глубины заложения пружин для участков с переменной глубиной заложения
От высоты воды HВ зависит выталкивающая сила, действующая на трубу и изменяется сопротивление грунта вертикальным и продольным перемещениям трубы (учитывается изменение свойств грунта, находящегося во взвешенном состоянии).
Для горизонтальных, вертикальных и наклонных под произвольным углом к горизонтальной плоскости участков при вычислении выталкивающей силы учитывается только та часть трубы, которая находится под водой (рис. 8).
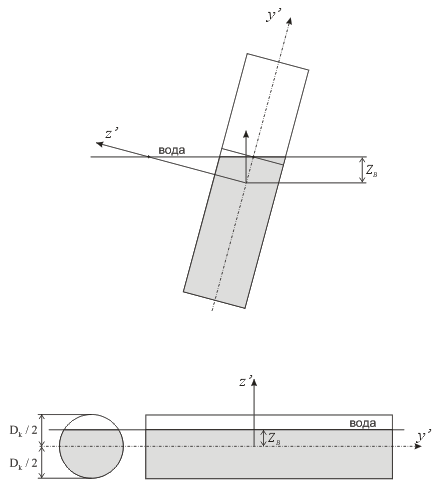
Рис. 8. Схемы к вычислению объема вытесненной жидкости для определения выталкивающей силы
При просадке, например, из-за оттаивания нижележащих слоев грунта или подработки по время проведения строительных работы вблизи трубопровода, трубопровод не испытывает со стороны основания отпора и перемещается вместе с грунтом вниз (рис. 9).
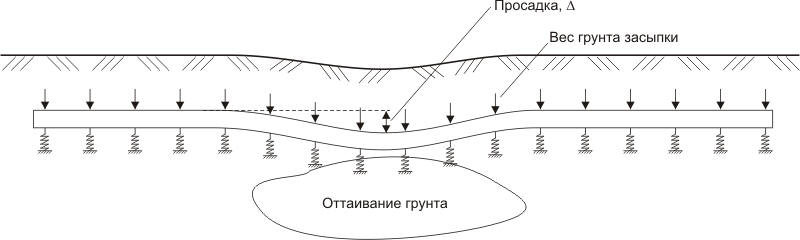
Рис. 9. Модель трубопровода при просадке грунта
Процесс просадки основания можно описать, сдвинув график зависимости, показанной на рис. 6, б влево на величину просадки основания Δ (рис. 10). Такая модель эквивалентна смещению пружин, моделирующих сопротивление грунта в вертикальной плоскости вниз (вдоль оси Z) на величину Δ (рис. 9).
Величину просадки в результате оттаивания и сжатия нижележащих слоев грунта можно определить, например, по СНиП [5] или по специальным программам БОРЕЙ, FROST 3D и т.д. и задание в программе СТАРТ-ПРОФ в свойствах трубы, защемленной в грунте, как смещение грунта по оси Z вниз.
Для моделирования морозного пучения грунта (вверх), величину просадки следует задать положительной по оси Z.
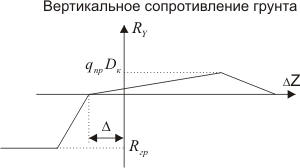
Рис. 10. Зависимость сопротивления грунта вертикальным перемещениям с учетом просадки
Для моделирования оползней, поперечных смещений грунта и прочих подобных явлений, смещения могут быть заданы также и в горизонтальном направлении.
Сопротивление грунта продольным перемещениям трубы в области упруго-пластических деформаций можно представить линейной зависимостью, предложенной А.Б. Айнбиндером [1].
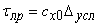
где
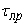- предельное сопротивление грунта сдвигу, н/см2,
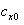- обобщенный коэффициент касательного сопротивления
грунта н/см3,
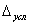- условное перемещение, соответствующее предельному
сопротивлению грунта сдвигу, см.
Зависимость получена путем замены истинной диаграммы сопротивления грунта продольным перемещениям (рис. 11, а) идеализированной билинейной диаграммой (рис. 11,б).
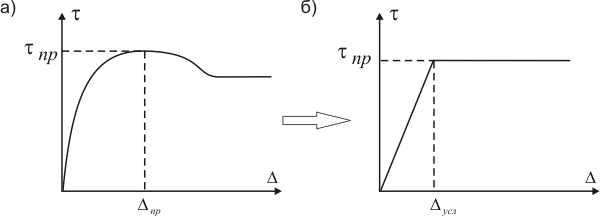
Рис. 11. Зависимость сопротивления грунта продольным перемещениям
Обобщенный коэффициент касательного сопротивления грунта представляет собой отношение
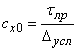
и имеет размерность коэффициента постели грунта при сдвиге. В нормативной базе по грунтам он сокращенно называется коэффициентом сопротивления продольным перемещениям. Коэффициент выражает наклон первого участка билинейной диаграммы, показанной на рис. 11, б.
Для того, чтобы задать жестко-пластическую модель грунта, без учета
упругой составляющей сопротивления, нужно задать коэффициент касательного
сопротивления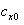
очень большим числом (рис. 12).
На практике можно использовать большое число, например 100000 тс/м3. Если в базе данных 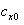=0, то в СТАРТ-ПРОФ автоматически принимается
его значение равное 100000
тс/м3.
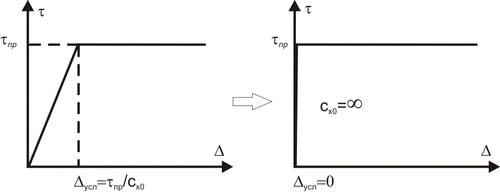
Рис. 12. Упруго-пластическая и жестко-пластическая модель грунта
Значения 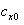, полученные в результате обработки экспериментальных
данных для некоторых типов грунтов, приведены в таблице
Значение обобщенного коэффициента касательного сопротивления грунта, кг/м3
Виды грунтов |
Пределы нормативных значений консистенции грунтов IL |
Характеристики грунтов при коэффициенте пористости ε |
||||
|---|---|---|---|---|---|---|
<0.5 |
0.5-0.6 |
0.6-0.7 |
0.7-0.8 |
>0.8 |
||
| Пески гравелистые, крупные и средней крупности | - | 330000 | 300000 | 270000 | 250000 | - |
| Пески мелкие и пылеватые | - | 250000 | 210000 | 210000 | 190000 | - |
| Супеси | 0 < IL ≤ 0.25 | 350000 | 330000 | 300000 | 300000 | 300000 |
| 0.25 < IL ≤ 0.75 | 350000 | 320000 | 300000 | 250000 | 250000 | |
| Суглинки | 0 < IL ≤ 0.3 | 380000 | 350000 | 350000 | 320000 | 300000 |
| 0.3 < IL ≤ 0.75 | 350000 | 330000 | 300000 | 250000 | 200000 | |
| Глины | 0 < IL ≤ 0.3 | 400000 | 380000 | 350000 | 330000 | 300000 |
| 0.3 < IL ≤ 0.75 | 450000 | 400000 | 350000 | 300000 | 300000 | |
При расчете по ГОСТ 55596-2013 и CJJ/T 81-2013 всегда используется жестко-пластическая модель грунта. Для всех остальных нормативных документов используется упруго-пластическая модель
1. Айнбиндер А.Б., Камерштейн А.Г. Расчет магистральных трубопроводов на прочность и устойчивость. М. “Недра”.1982 г.
2. Скоморовский Я.З., Айнбиндер А.Б., Продольные перемещения подземных трубопроводов с учетом физической нелинейности сопротивления грунта при сдвиге. Вопросы прочности трубопроводов 1975 г, (Труды ВНИИСТ, вып. 25).
3. Arbeitsblatt FW 401: Verlegung und static von KMR für Fernwärmenetze Arbeitsgemeinschaft Fernwärme- AGFW-e, V.- bei der Vereinigung Deutscher Elektrizitätswerke, 1992.
4. Бородавкин П.П., Подземные магистральные трубопроводы (проектирование и строительство), М. “Недра”, 1982
5. СНиП 2.02.04–88. Основания и фундаменты на вечномерзлых грунтах. Госстрой СССР. - М. АПП ЦИТП, 1991
6. Айнбиндер А.Б., Камерштейн А.Г. Расчет магистральных и промысловых трубопроводов на прочность и устойчивость. М. "Недра".1991 г.