Tees and stub-ins connect two cylindrical shells and include these types:
Welding Tee per ASME B16.9 - manufactured by pressing steel sheets and welding halves together
Fabricated Tee - factory-welded from two pipes
Stub-in - field-welded connection of two pipes
Custom Tee - user-defined flexibility and stress intensification factors
Thermoplastic Tee - GRP or plastic tee
Weldolet - welded branch connection fitting
Sweepolet - contoured welded insert
Extruded Outlet - formed by pulling a ball through pipe wall
Cross - four-way pipe connection
ASME code features:
START-PROF does not check tee wall thickness for ASME codes. Russian code compliance includes wall thickness checks for all tee types.
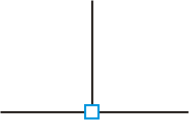
Without a tee element at a node, the joint models as three connected pipes without rigidity elements, flexible hinges, or tee stress calculation.

Fig. 1. Pipe intersection without tee element
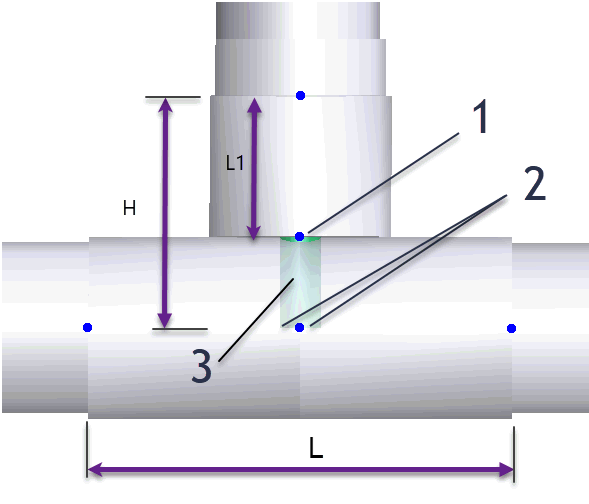
Adding any tee type to the intersection node enables specification of tee length (L), height (H), header wall thickness, and branch wall thickness.
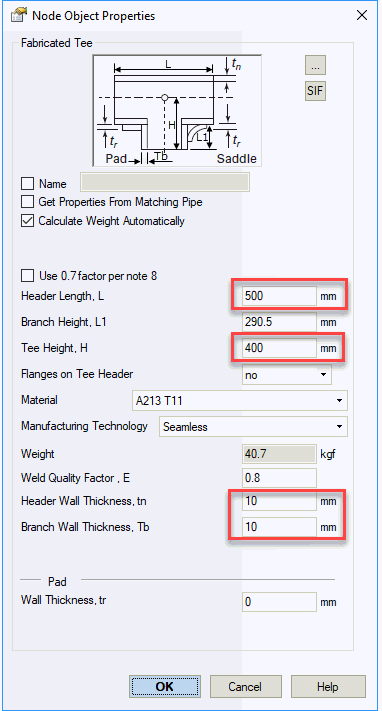
Leaving tee length (L) and height (H) blank inserts a rigid element (H=Dh/2, where Dh is header outer diameter) with zero weight for element, fluid, and insulation.
During analysis, the simple tee model converts to a complex model with six additional nodes (21, 2, 3, 4, 5, 20). These nodes remain hidden except in developer mode.
Element 10-20 is rigid (H=Dh/2). Weight components are zero
Elements 4-10 and 10-5 have 1 mm length (L=2mm)
Pipe element 20-21 uses wall thickness from tee dialog (Tb=10 mm default)
Pipe elements 4-3 & 5-2 use wall thickness from tee dialog (tn=10 mm default)
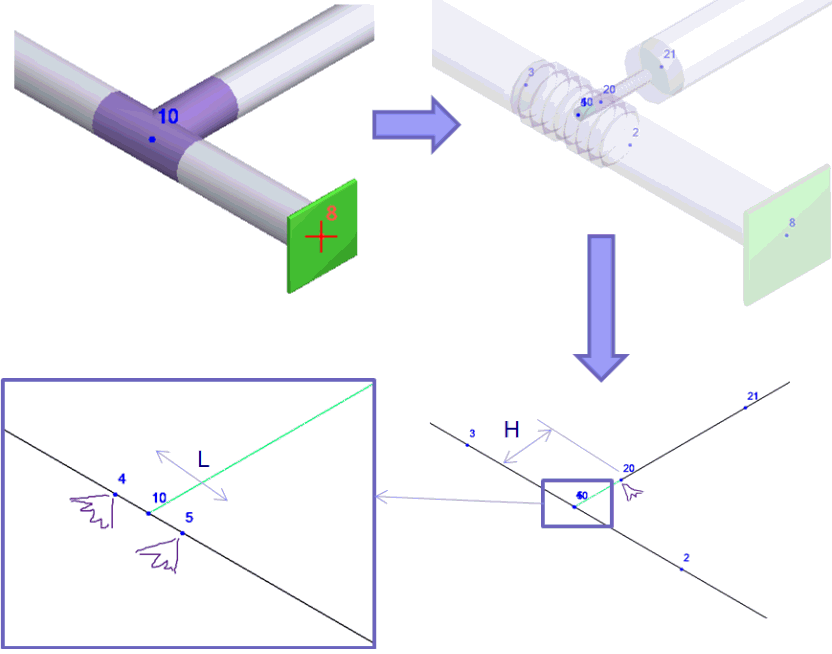
Tee object model as displayed in START-PROF:
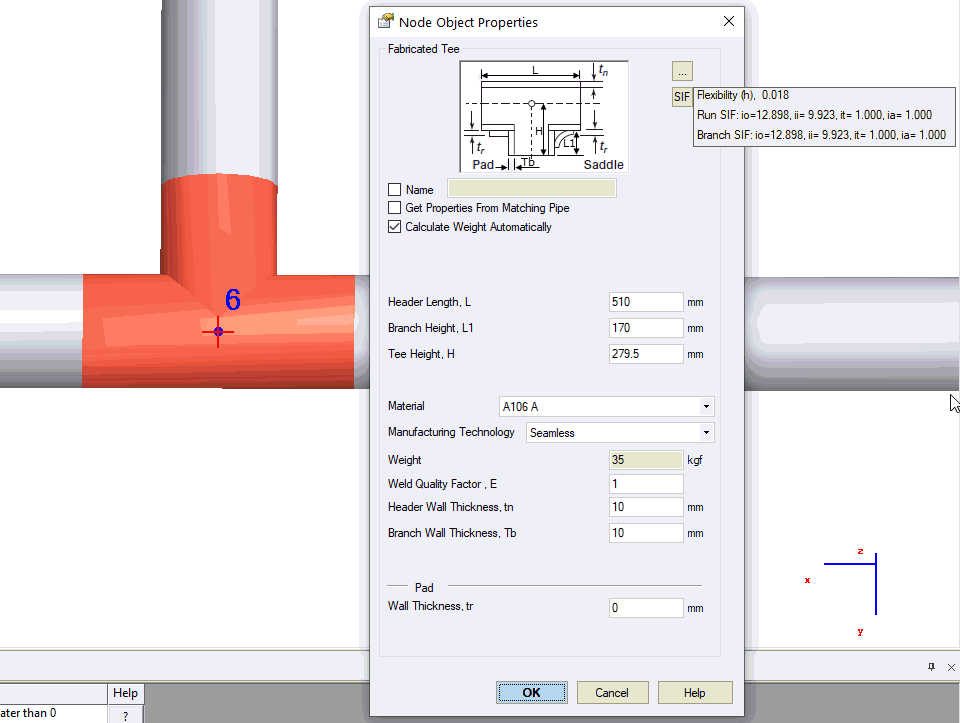
Internal tee model used for analysis. Header and branch pipes may have different wall thickness than connected pipes. Flexible springs model header (2) or branch (1) flexibility per ASME B31J. Rigid element (3) eliminates branch flexibility artifacts.
For Custom Tee and standard tees using ASME B31J, run flexibilities add to nodes 4 & 5, branch flexibilities to node 20, calculated per ASME B31J.
With "Consider Tee Branch Flexibility" enabled, nodes 4 & 5 omit for standard tees. Node 20 flexibilities calculate per the standard selected in Project Settings. ASME and DL/T 5366-2014 use ASME BPV SIII div 1 class 1 NB 3686 for reducing tees with Db/Dh<0.5. Russian codes apply to Db/Dh<0.8.
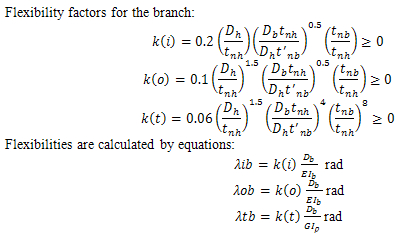
Tee weight Q distributes along header length L: q=(Q-qp*L1)/L, where qp is branch-connected pipe weight, L1=H-D/2 is branch length. Rigid element length is zero. Tee-covered pipe weight subtracts. Insulation and product weights match connected pipes. Snow, ice, wind, and user uniform loads inherit from connected pipes.
Tee stress calculation uses stress intensification factors (SIFs) that indicate stress magnification relative to basic pipe bending stress. SIF formulas follow applicable standards. Equivalent stress calculates for three cross-sections 1, 2, and 3 (Fig. 3). The maximum value governs the analysis.
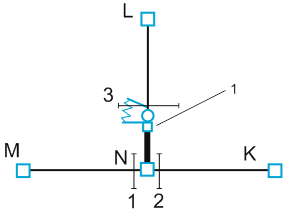
1 - automatically added hidden node
Fig. 3. Tee stress analysis cross-sections (1,2,3)
To insert a tee, select the node and use: Insert > Tee
To view element properties:
Double-click the element in the 3D view
Select the
element and click  toolbar icon
toolbar icon