Граничные условия гидравлического расчета
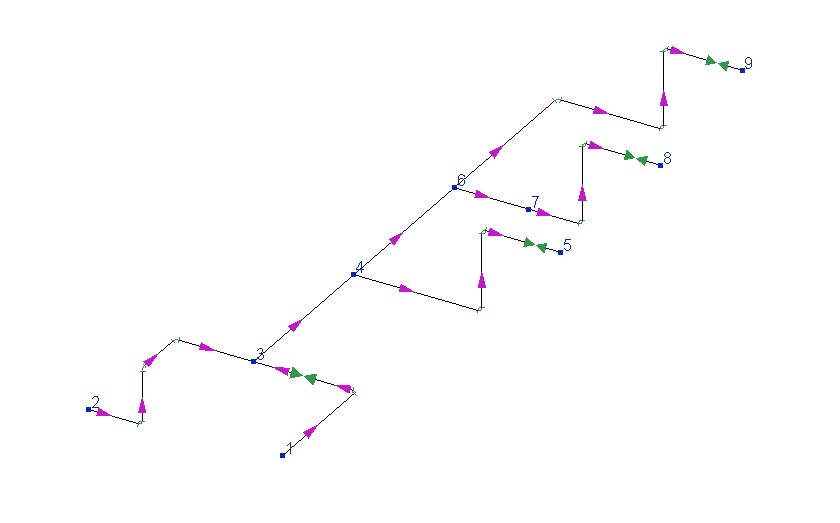
Постановка задачи гидравлического (изотермического или теплового) расчета может быть различной в зависимости от того, что является целью расчета. А цели у расчета в свою очередь могут быть совершенно разные - расчет пропускной способности и распределения потоков, расчет потерь давления "по потоку", "против потока" и т.д. В качестве примера рассмотрим трубопроводную систему ниже, состоящую из следующего набора ветвей* (о делении трубопровода на ветви подробно описано тут), геометрическая конфигурация которых (включая значения диаметров) полностью известна:

| Ветвь | Начальный узел | Конечный узел |
|
Ветвь A |
1 |
3 |
|
Ветвь B |
2 |
3 |
|
Ветвь C |
3 |
4 |
|
Ветвь D |
4 |
5 |
|
Ветвь E |
4 |
6 |
|
Ветвь F |
6 |
7 |
|
Ветвь G |
7 |
8 |
|
Ветвь H |
6 |
9 |
Для большей наглядности рассмотрим случай, в котором в промежуточных узлах нет притоков/оттоков потока**. Гидравлический расчет данного трубопровода сводится к решению следующей системы уравнений:
P1 - P3 = f(QA);
P2 - P3 = f(QB);
P3 - P4 = f(QC);
P4 - P5 = f(QD);
P4 - P6 = f(QE);
P6 - P7 = f(QF);
P7 - P8 = f(QG);
P6 - P9 = f(QH);
QA + QB - QC = 0;
QC - QD - QE = 0;
QE - QF - QH = 0;
QF - QG = 0
где Pi - давление в соответствующем узле i, QN - расход в ветви N трубопровода.
Данная система состоит из 12 уравнений: первые 8 из них описывают взаимосвязь потерь давления в каждой из 8 ветвей данного трубопровода от расходов продукта в этих ветвях (о том, как потери давления зависят от расходов, см. тут), остальные 4 описывают баланс расходов в промежуточных узлах трубопровода (сумма расходов входящих в узел потоков равна сумме исходящих). Как видно, переменных в этой системе всего 17 - величины давлений в 9 узлах и расходов в 8 ветвях трубопровода. Поэтому чтобы данная система уравнений была однозначно определена и имела одно единственное решение, необходимо зафиксировать значения 5 ее независимых (!) переменных. Таким образом количество неизвестных в системе уравнений будет равно количеству решаемых уравнений. Переменные системы, значения которых принимаются в расчете известными, называют граничными условиями гидравлического расчета. В Гидросистеме граничные условия указываются в виде задания в исходных данных для соответствующих ветвей и узлов трубопровода известных величин давлений и/или расходов. Давления и расходы во всех остальных узлах/ветвях трубопровода рассматриваются неизвестными и в исходных данных не задаются - они будут определены при решении описанной выше системы уравнений.
Варианты постановки задачи гидравлического расчета
В зависимости от того, какие параметры потока в гидравлическом расчете принимаются известными (т.е., какие граничные условия задаются), различают несколько вариантов постановки задачи гидравлического расчета, среди которых наиболее распространенными на практике являются следующие:
"поверочный" расчет (или расчет потерь давления по ходу движения потока) - граничными условиями для такого расчета являются известные величины давлений во всех начальных точках трубопровода (в узлах 1 и 2 для примера выше) и известные расходы продукта во всех конечных ветвях трубопровода (для примера выше это ветви D, G и H). Давления и расходы во всех остальных узлах/ветвях трубопровода в этом случае задавать не нужно - они будут определены при решении описанной выше системы уравнений. Такая постановка задачи используется в тех случаях, когда известно давление продукта в начале трубопровода (к примеру, продукт перекачивается насосом, напор которого известен или продукт подается из бака с известным уровнем жидкости и т.д.) и нужно определить, насколько давление упадет к каждой из конечной точек трубопровода при перекачке определенного (заданного) расхода продукта;
"обратный" поверочный расчет (или расчет потерь давления против хода движения потока) - граничными условиями для такого расчета являются известные величины давлений во всех конечных точках трубопровода (в узлах 5, 8 и 9 для примера выше) и известные расходы продукта во всех начальных ветвях трубопровода (для примера выше это ветви A и B). Давления и расходы во всех остальных узлах/ветвях трубопровода в этом случае задавать не нужно - они будут определены при решении описанной выше системы уравнений. Такая постановка задачи используется в тех случаях, когда нужно, чтобы продукт дошел до потребителя/потребителей с определенным (известным) давлением и требуется определить, какое для этого должно быть давление в начале трубопровода (к примеру, чтобы затем подобрать по этому давлению насос) при перекачке определенного (заданного) расхода продукта;
расчет пропускной способности трубопровода (или расчет расходов) - граничными условиями для такого расчета являются известные величины давлений во всех начальных и конечных точках трубопровода (в узлах 1, 2, 5, 8 и 9 для примера выше). Давления во всех остальных узлах трубопровода, а также расходы во всех ветвях трубопровода в этом случае задавать не нужно - они будут определены при решении описанной выше системы уравнений. Такая постановка задачи используется, когда давления на границах трубопровода фиксированы и нужно определить, какой расход может "пропустить" данный трубопровод (и как распределятся потоки) при заданной разнице давлений.
Возможны и другие варианты постановки задачи гидравлического расчета - к примеру, когда для части начальных и конечных точек трубопровода известны расходы, для других - давления или когда давления по каким-то причинам известны в некоторых промежуточных точках и т.д. Такие задачи в Гидросистеме также можно решить, задав для расчета соответствующие граничные условия, однако, на практике такие задачи встречаются крайне редко.
Как не следует задавать граничные условия гидравлического расчета
Как уже упоминалось выше, для расчета система уравнений должна быть определенной - то есть, число уравнений должно быть равно числу неизвестных в системе. Чтобы обеспечить определенность системы, достаточно соблюдать следующее правило - для каждой начальной и конечной точки трубопровода необходимо задать либо значение давления, либо расхода (для приведенного выше примера трубопровода, у которого 2 начальные и 3 конечные точки, в этом случае задаются значения как раз 5 переменных - ровно столько, сколько необходимо для "замыкания" данной системы). Если при этом хотя бы для одной начальной или конечной точки трубопровода не задано ни величины давления, ни расхода, то такая система является недоопределенной (то есть, в ней число неизвестных больше числа уравнений, и она будет иметь бесконечное множество решений). Это легко видеть, если для приведенного выше примера трубопроводной системы, к примеру, не задать в качестве граничных условий ни давление в узле 1, ни расход в ветви A (начинающейся в этом узле). В этом случае решить первое уравнение "P1 - P3 = f(QA)" в этой системе не удастся (даже если путем решения остальных уравнений в системе удастся однозначно определить величину P3), так как в этом уравнении будут две неизвестные***. Другими словами, расход потока, идущий от узла и давление в этом узле - это взаимосвязанные величины (связь между которыми для данного узла описывается уравнением "P1 - P3 = f(QA)", для других узлов - аналогичными уравнениями). Если известно давление в узле 1, то значение расхода в ветви A тем самым уже определено (оно будет тем больше, чем выше давление в узле). И наоборот, если известен расход в ветви A, то его величина определяет то, каким будет давление в узле (оно будет тем больше, чем больше значение расхода). То же самое касается и конечных узлов трубопровода - расход потока, идущий к конечному узлу, напрямую связан (через соответствующее уравнение потерь давления) с давлением в этом узле. Поэтому чтобы рассчитываемая система имела единственное решение, для каждой начальной и конечной точки трубопровода одна из величин (давление или расход) должна быть известна и задана в исходных данных для расчета, другая - неизвестна и не задана.
Если же наоборот, хотя бы для одной начальной или конечной точки трубопровода заданы величины и давления, и расхода, то в этом случае система становится переопределенной (при условии что для всех остальных начальных и конечных точек задано либо давление, либо расход, иначе как описано выше, система будет недоопределенной). В такой системе число неизвестных меньше числа уравнений, и она не будет иметь решений. То есть, такая постановка задачи, когда для одной и той же начальной/конечной точки трубопровода известны и величина давления, и расхода, является некорректной - данные величины, как уже упоминалось выше, являются зависимыми друг от друга, и при задании обеих из них, их значения могут вступать в противоречие друг с другом. Чтобы избежать такого рода некорректных постановок задач, в программе действует следующее правило - заданная величина давления в узле имеет бОльший приоритет по сравнению с величиной расхода в примыкающей к нему ветви. Поэтому если для какой-то начальной или конечной точки трубопровода задано и давление, и расход, то введенное значение расхода игнорируется и пересчитывается, каким оно будет при заданном давлении в узле. Как уже упоминалось выше, расход в этом случае однозначно определяется величиной давления.
Из всего вышесказанного логично вытекают несколько важных фактов:
в качестве граничных условий гидравлического расчета необходимо выбирать только независимые друг от друга переменные, иначе их значения могут противоречить друг другу, из-за чего некоторые из этих параметров (значения расходов) будут отброшены и пересчитаны при решении системы уравнений (то есть, не будут восприняты как граничные условия);
обеспечение в начальной или конечной точке трубопровода одновременно и заданного значения давления, и желаемой величины расхода "само по себе" невозможно. К примеру, если в конечной точке трубопровода величина давления фиксирована, то расход потока к этой точке пойдет не такой, какой "нужен проектировщику", а какой "сам захочет". Как говорится, "поток не дрессированный", и он распределяется в трубопроводе исходя из сопротивлений ветвей трубопровода и значений давлений в точках от/к которым он идет, а не исходя из наших пожеланий. Поэтому единственный способ обеспечить одновременно в начальной/конечной точке трубопровода и заданное давление, и требуемый расход - это регулировать расход потока с помощью регулирующих клапанов или других регулирующих устройств;
задание давлений в промежуточных узлах трубопровода может привести к возникновению дисбаланса расходов в данном узле (то есть, сумма расходов входящих в этот узел потоков не будет равна сумме исходящих). Связано это с тем, что как уже упоминалось выше, величина давления в узле имеет бОльший по сравнению с величиной расхода приоритет в расчете. Таким образом, если в промежуточном узле задано давление, то расходы в примыкающих к этому узлу ветвях будут пересчитываться по данной величине давления, в результате чего сумма притоков/оттоков в узле может не быть равной нулю. Поэтому не рекомендуется при расчете задавать давления в промежуточных узлах трубопровода, если только это не аргументировано особенностями постановки решаемой задачи (такое, к примеру, может встретиться, если в некотором промежуточном узле заканчиваются несколько ветвей, но ни одна не начинается или наоборот, начинаются несколько ветвей, но ни одна не заканчивается. Для таких узлов в некоторых случаях задаются давления, так как с точки зрения расчета такой узел рассматривается как, соответственно, узел-потребитель или узел источник).
Обратите внимание, что в качестве граничных условий гидравлического расчета допускается задание только давлений или расходов на границах трубопроводной системы (т.е., в начальных и конечных точках). Заданные в исходных данных расходы в промежуточных ветвях трубопровода (не являющихся начальными или конечными) при расчете рассматриваются исключительно в качестве начальных приближений и не могут являться граничными условиями гидравлического расчета. Более того, если к примеру, речь идет о трубопроводах с замкнутыми контурами (трубопроводы с кольцами, рециклами и т.д.), то расходы в промежуточных ветвях такого трубопровода почти всегда пересчитываются в ходе расчета. Это связано с тем, что распределение потоков в ветвях замкнутых контуров определяется исключительно геометрией (сопротивлением) элементов, входящих в состав этих ветвей, и таким образом расходы в таких ветвях определяются автоматически при решении системы уравнений, описывающей данный трубопровод. Поэтому как уже упоминалось выше, расход в ветвях замкнутого трубопровода "сам по себе" не установится таким, как требуется (согласно технологии процесса) - для того, чтобы расход в таких ветвях был равен требуемому, необходимо его регулировать с помощью регулирующих клапанов или других регулирующих устройств.
Особенности постановки задачи и граничных условий проектного расчета трубопровода
В отличие от изотермического и теплового расчета трубопровода целью проектного расчета является определение требуемых диаметров ветвей трубопровода (которые при изотермическом и тепловом расчете полагаются известными). Поскольку потери давления в трубопроводе зависят также и от величин диаметров, в систему уравнений для приведенного выше примера трубопровода при проектном расчете добавляются новые переменные (величины диаметров каждой из ветвей), и эта система перезаписывается следующим образом:
P1 - P3 = f(QA, DA);
P2 - P3 = f(QB, DB);
P3 - P4 = f(QC, DC);
P4 - P5 = f(QD, DD);
P4 - P6 = f(QE, DE);
P6 - P7 = f(QF, DF);
P7 - P8 = f(QG, DG);
P6 - P9 = f(QH, DH);
QA + QB - QC = 0;
QC - QD - QE = 0;
QE - QF - QH = 0;
QF - QG = 0
где Pi - давление в соответствующем узле i, QN - расход в ветви N трубопровода, DN - диаметр ветви N.
В данной системе по прежнему 12 уравнений, но на этот раз в ней 25 переменных - величины давлений в 9 узлах, величины расходов в 8 ветвях и значения диаметров 8 ветвей трубопровода. Поэтому чтобы данная система уравнений была однозначно определена и имела единственное решение, необходимо зафиксировать значения 13 из этих переменных. Обычно постановка задачи проектного расчета формулируется таким образом, что известно, с каким давлением продукт подается в трубопровод (в начальных точках), с каким давлением продукт должен дойти до каждого из потребителей (конечных точек) и какой расход продукта должен перекачиваться в каждой из ветвей трубопровода. Поэтому граничными условиями проектного расчета всегда являются давления во всех начальных и конечных точках трубопровода и расходы продукта во всех без исключения ветвей трубопровода (для приведенного выше трубопровода это будут давления в 2 начальных, 3 конечных узлах и расходы в 8 ветвях - итого 13 переменных). Давления в промежуточных узлах и диаметры ветвей трубопровода рассматриваются неизвестными и в исходных данных не задаются - они будут определены при решении описанной выше системы уравнений.
Важно понимать, что если хотя бы одно из указанных выше граничных условий не задано, это сразу же делает решаемую систему уравнений недоопределенной. К примеру, если для приведенной выше схемы трубопровода при проектном расчете не указать давление в узле 9, это сразу же делает неопределенной величину диаметра ветви H - поскольку для этой ветви можно подобрать "любое" (в рамках разумного) значение диаметра и с данным значением получится какое-то значение давления в узле 9 (то есть, система будет иметь бесконечное множество решений). Другими словами, то, каким нужно брать значение диаметра данной ветви зависит от того, какое давление требуется получить в конце этой ветви (аналогично и для других узлов/ветвей трубопровода).
Теоретически выбор диаметров может также иметь такую постановку задачи, при которой давления известны не в начальных/конечных узлах системы, а в каких-либо промежуточных точках трубопровода. Однако, практического интереса такие задачи не представляют, поэтому в расчетах в Гидросистеме они не рассматриваются. Исключением разве что являются случаи, в которых в некотором промежуточном узле заканчиваются несколько ветвей, но ни одна не начинается или наоборот, начинаются несколько ветвей, но ни одна не заканчивается. В этом случае при выборе диаметров в таком узле необходимо задать давление, так как с точки зрения проектного расчета такой узел рассматривается как, соответственно, узел-потребитель или узел источник.
Обратите внимание, что в отличие от изотермического и теплового расчетов, в которых величины расходов в промежуточных ветвях трубопровода рассматриваются исключительно как начальные приближения для расчета и не более, при проектном расчете расходы во всех ветвях являются граничными условиями для расчета, поэтому их необходимо задавать в исходных данных для всех ветвей, в том числе и промежуточных. Это связано с тем, что для некоторых видов схем трубопроводов расходы на промежуточных ветвях не определяются однозначно величинами расходов в начальных и конечных ветвях трубопровода. Ниже приведен пример такой схемы:
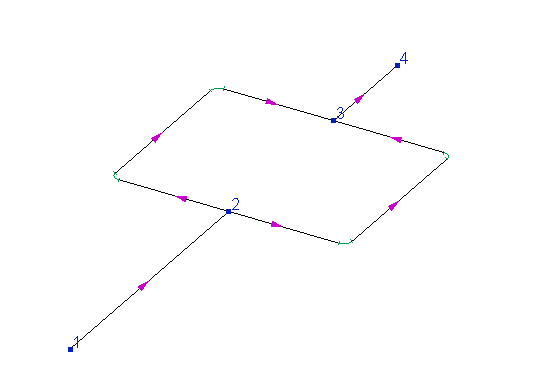
В данном трубопроводе поток может делиться в узле 2 на две, к примеру, равные части, или же бОльшая часть потока может пойти по "левой" ветви замкнутого контура, а меньшая по "правой" и т.д. И в зависимости от того, как должны быть распределены потоки между "левой" и "правой" ветвью замкнутого контура данного трубопровода, диаметры для этих ветвей нужно выбирать разные (если нужно, чтобы потоки делились поровну, то диаметры этих ветвей должны быть одинаковы; если нужно, чтобы бОльшая часть потока шла по "левой" ветви, то у этой ветви диаметр должен быть больше, чем в правой и т.д.). Именно поэтому при проектном расчете желаемые расходы продукта необходимо указывать для всех ветвей трубопровода, включая промежуточные.
Кроме того, выбор диаметров на практике довольно часто осуществляется исходя из соображений ограничения скоростей движения продукта в трубопроводе, то есть, для труб подбираются наименьшие диаметры, при которых скорости движения продукта не превышают максимально допустимых значений. В Гидросистеме такой расчет также предусмотрен, однако даже при такой постановке задачи выбора диаметров граничные условия задаются точно так же, как описано выше.
Особенности задания граничных условий при расчете трубопроводов с регулирующими клапанами
Элемент "Регулирующий клапан" используется в гидравлическом расчете для регулирования заданной величины расхода продукта и определения параметров настройки регулирующего клапана, необходимых для поддержания данной величины расхода. Соответственно, в ходе расчета определяется, какой перепад давлений должен быть на данном клапане, чтобы расход в этой ветви был равен требуемому. Упрощенно алгоритм этого расчета можно представить следующим образом: схема трубопровода как бы "разрезается" на две части в месте установки каждого из регулирующих клапанов; каждая из полученных таким образом частей считается отдельно (как отдельный трубопровод) независимо от остальных частей; граничным условием в "точке разрезания" полагается известная величина расхода, заданная на регулирующем клапане. В расчете каждой части такого трубопровода определяется давление в "точке разрезания", таким образом можно определить давление до и после каждого регулирующего клапана. Ну и соответственно, разница между давлениями до и после клапана (полученными для этой точки в расчетах двух частей трубопровода - до регулятора и после него) и является требуемым перепадом давления на регулирующем клапане.
В связи с особенностями моделирования регулирующих клапанов, граничные условия для расчета в этом случае необходимо задавать таким образом, чтобы давление было известно (хотя бы в одной точке) в каждой из частей, на которые "разрезается" модель трубопровода в месте установки регуляторов. В противном случае расчет данной части не представляется возможным. Или говоря другими словами, величина перепада давления на регулирующем клапане, требуемого для поддержания заданного значения расхода, зависит как от давления в части системы до этого клапана, так и в части после него. Поэтому не зная давления в одной из этих частей невозможно определить требуемый перепад давлений на регуляторе. Более наглядно это показано на примере ниже:
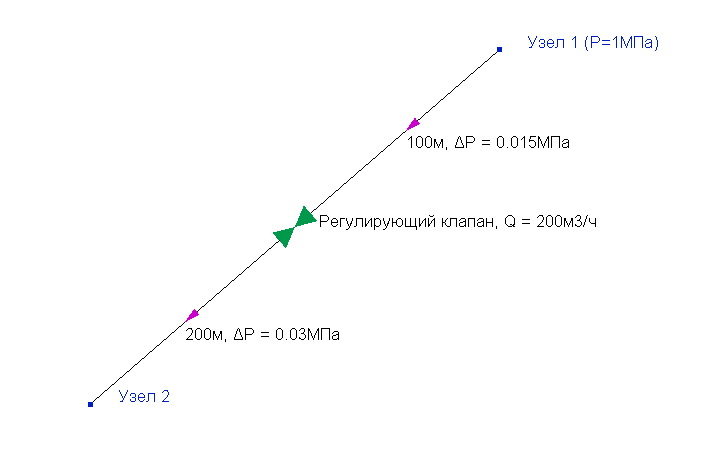
На этом рисунке изображен пример трубопровода, в котором продукт перекачивается из узла 1 (с давлением 1МПа) в узел 2; расход потока при этом поддерживается равным 200м3/ч с помощью регулирующего клапана. Потери давления на участках трубопровода до и после регулирующего клапана при данном расходе составляют, соответственно, 0.015 и 0.03МПа. Таким образом, как видно, в узле 2 этого трубопровода давление может быть практически любой величины ниже 0.955МПа (1 - 0.015 - 0.03 МПа). К примеру, если давление во 2-ом узле 0.5МПа, это означает, что перепад давления на регулирующем клапане должен быть равен 1 - 0.5 - 0.015 - 0.03 = 0.455МПа. А если давление во 2-ом узле будет, например 0.7МПа, то перепад давления на клапане при этом должен быть 1 - 0.7 - 0.015 - 0.03 = 0.255МПа и т.д. То есть, регулятор может поддерживать требуемый расход при любой разнице давлений на границах системы (только в разумных пределах - об этом см. следующий абзац). Просто в зависимости от этой разницы параметры настройки клапана (перепад давления на нем и величина его коэффициента пропускной способности Kv в "настроенном" состоянии) будут разными. Поэтому чтобы их определить, необходимо знать давление в какой-либо точке системы и до, и после клапана.
Обратите внимание, что в Гидросистеме можно также моделировать работу регулирующего клапана в невозможном для него режиме, а именно, чтобы на нем возникал отрицательный перепад давления. К примеру, такое может возникнуть, если для трубопровода на рисунке выше задать давление в узле 2, например, 1.5МПа. Как легко видеть, перепад давления на регулирующем клапане в этом случае получится 1 - 1.5 - 0.015 - 0.03 = -0.545МПа. То есть, клапан должен не создавать дополнительное сопротивление, а наоборот - повышать напор перекачиваемой среды на соответствующую величину. Конечно же, реальный регулирующий клапан на такое не способен (клапан может только уменьшать напор), но в расчете такая ситуация допускается - программа в этом случае выдаст соответствующее сообщение в протокол расчета (об отрицательном перепаде давлений на клапане), но при этом все рассчитает. В частности, данную возможность удобно использовать в тех случаях, когда требуется рассчитать, какой дополнительный напор нужно придать перекачиваемой среде, чтобы обеспечить для нее требуемый расход (к примеру, при расчете требуемого напора насоса). Так что если в результате расчета трубопровода с регулирующим клапаном оказалось, что потери давления на клапане отрицательные, это означает, что для поддержания заданного расхода продукта нужно устанавливать не регулирующий клапан ("пережимающий" поток в трубопроводе), а дополнительный подкачивающий насос с напором, равным модулю рассчитанного для регулирующего клапана перепада давлений.
Граничные условия расчета гидроудара
Задание граничных условий для расчета гидроудара подробно описано в соответствующем разделе.
________________________________________________
* - данная схема рассматривается исключительно в качестве примера. Все приведенные рассуждения и выводы будут справедливо для трубопроводов с абсолютно любой топологией (разветвленных, неразветвленных, с одой или несколькими начальными/конечными точками, с замкнутыми контурами и без и т.д.), в чем каждый может легко убедиться, составив данную систему уравнений для любого интересующего трубопровода.
** - при наличии притоков/оттоков в промежуточных узлах принципиально в системе уравнений для данного трубопровода ничего не поменяется. Только в правой части каждого из четырех последних уравнений будет не ноль, а величина притока/оттока в соответствующем узле, которая в этом случае задается в программе и является известной величиной в расчете.
*** - внимательный читатель в этом месте может возразить, что данная система все же может иметь единственное решение, если расход QA можно определить по уравнению баланса расходов в узле 3, к примеру, если расходы QB и QC заданы явно, либо могут быть определены косвенно по расходам в остальных ветвях трубопровода. Однако, это означает, что и пользователь программы в этом случае может сам с легкостью сосчитать расход QA и задать его в исходных данных в программе. Поэтому во избежание ненужного усложнения расчетного алгоритма программы, допускаются только такие варианты постановки задачи, в которых для каждой начальной и конечной точки трубопровода задана либо величина давления, либо расхода.