Гидравлический расчет двухфазного газожидкостного течения

Расчет газожидкостного течения может выполняться без учета массообмена между фазами (так называемое "замороженное" течение) или с расчетом массообмена (то есть с учетом испарения и конденсации продукта по ходу течения). Расчет "замороженного" течения возможен как для изотермического течения, так и для совместного теплового и гидравлического расчета. Расчет с учетом массобмена между фазами возможен только при совместном тепловом и гидравлическом расчете. Для выполнения данного расчета требуется расчет фазового равновесия, поэтому расчет возможен лишь при задании продукта с использованием библиотек СТАРС, WaterSteamPro (Вода/пар по IAPWS-IF97), GERG-2008 или Simulis Thermodynamics.

Для газожидкостных потоков течение считается установившимся, а фазы – находящимися в состоянии термодинамического равновесия и имеющими одинаковые температуру и давление. При этом может учитываться "проскальзывание" жидкой и газовой фаз, то есть их движение с разными скоростями. В процессе гидравлического расчета двухфазного потока для всех участков производится расчет:

• режима двухфазного течения в различных точках трубопровода;

• истинного объемного газосодержания (и на его основе расчет истинных скоростей фаз, а также гидростатических потерь на участках с перепадом высот);

• потерь на трение;

• потерь на местных сопротивлениях;

• потерь на ускорение потока;

• величины числа Маха.

Для определения режимов течения и выполнения расчета могут использоваться различные методики. Поскольку методы расчет двухфазных потоков в настоящее время интенсивно развиваются, и на сегодняшний момент не существует какого-то универсального общепризнанного подхода, в программе для наиболее важных решаемых задач реализована не одна, а целый набор методик, из которых можно выбрать наиболее подходящие для конкретной ситуации в соответствии с потребностями пользователя. При этом предусмотрена возможность достаточно гибко управлять тем, какие именно методики использовать для различных типов участков в различных случаях, с помощью специальных правил выбора методов двухфазного расчета. Пользователь может использовать собственные правила или воспользоваться одними из уже настроенных, входящих в состав поставляемой программы.

Режимы течений

Определение режима двухфазного течения выполняется по наиболее популярным в последнее время так называемым "механистическим" моделям, основанным на моделировании физических механизмов смены режима течения. Программа различает и определяет 6 режимов течения: расслоенный гладкий, расслоенный волновой, прерывистый (перемежающийся), пузырьковый, дисперсно-пузырьковый, кольцевой. В настоящее время программа не различает различные разновидности данных режимов, например разновидности прерывистого течения (такие как снарядное, пробковое и вспененное) или кольцевого течения (дисперсно-кольцевое, волновое кольцевое или клочковато-кольцевое), такую возможность планируется добавить в будущем.

Рассчитанные режимы течения можно использовать для более адекватного выбора методик расчета истинного объемного газосодержания и потерь давления. В дальнейшем планируется добавить в программу специализированные расчетные методики этих величин на основе моделей тех или иных режимов течения.

Дополнительно к определению режима двухфазного течения программа также позволяет диагностировать возможность возникновения "агрессивного перемежающегося двухфазного течения", вызванного накоплением жидкой фазы перекачиваемого продукта в отдельных элементах трубопровода. Обычно такое накопление происходит в конце протяженных горизонтальных или наклоненных вниз участках трубопровода, после которых следует подъем продукта на вертикальных трубах. В этом случае накопление жидкой фазы перед подъемом может вызывать полное перекрытие сечения трубы жидкостью, вследствие чего перекачка будет осуществляться эдакими периодическими "выстреливающими" порциями. Такой режим течения является нежелательным, поскольку он вызывает вибрации трубопровода и примыкающих к нему объектов, а также приводит к неравномерности перекачки газожидкостной смеси. Возможность возникновения агрессивного перемежающегося течения в Гидросистеме определяется в соответствии с методиками, изложенными в [32-39].

Истинное объемное газосодержание

Для расчета истинного объемного газосодержания в программе реализован целый ряд типов корреляций: HEM (однородная равновесная модель течения), корреляции степенного типа, корреляции на основе потока дрейфа и наиболее популярные эмпирические корреляции. Корреляции степенного типа в настоящее время представляют скорее исторический интерес и реализованы для совместимости с другими программами. Для больших и средних скоростей потока можно рекомендовать использовать корреляцию Premoli, а при небольших скоростях – подходящие по углу наклона потока корреляции Rouhani, Dix-Ghajar-Woldesemayat или Goda-Hibiki-Kim-Ishii-Uhle. Сравнительный обзор применимости и точности различных методик можно найти в [21].

Рассчитанное истинное объемное газосодержание используется при расчете потерь на перепадах высот, а также некоторых выводимых величин (истинных скоростей фаз и др.).

Потери на трение

Для расчета потерь на трение газожидкостного потока в программе реализованы два типа корреляций – на основе модели однородного течения и с использованием двухфазных мультипликаторов.

Первая группа методик рассчитывает потери на трение как для однофазного потока с теплофизическими свойствами газожидкостной смеси. Двухфазность течения при этом учитываются при расчете вязкости смеси (в методике Beattie – Whalley) или числа Рейнольдса смеси (в методике Shannak).

Во второй группе методик рассчитываются потери на трение для однофазного течения (для жидкой или газовой фазы) с последующей корректировкой на множители, учитывающие газосодержание и свойства фаз. При реализации в программе методик Friedel и MSH их возможности несколько расширены по сравнению с авторскими вариантами путем применения для расчета коэффициента гидравлического трения формулы Черчилля (как это рекомендуется в [13]), что позволяет применять их на всем диапазоне значений числа Рейнольдса, а также учесть влияние шероховатости стенок труб. Также приводятся рекомендации по применению методик двухфазных мультипликаторов, предложенные Whalley [2]. Более детальные рекомендации также предложены в [27].

Местные сопротивления

Вопрос расчета потерь давления на местных сопротивлениях для газо-жидкостного течения до сих пор современными исследователями изучен недостаточно. В текущей версии программы реализованы основные предложенные для этого случая в литературе методы расчета, представляющие собой разновидности метода двухфазных мультипликаторов для местных сопротивлений. Рекомендации по применению данных методов для различных видов местных сопротивлений даны в [13, 30, 31]. Для типов местных сопротивлений, для которых рекомендации отсутствуют, применяется методика HEM.

Динамические потери

Потери на ускорение потока рассчитываются с использованием модели HEM в соответствии с рекомендацией [1] для адиабатического течения.

Числа Маха

Число Маха для "замороженного" течения рассчитывается по модели однородного "замороженного" течения. При этом используется "изотермическая" скорость звука в газовой фазе. Для течения с учетом массообмена число Маха рассчитывается по модели HEM.

Вязкость смеси

Расчет средней вязкости газожидкостной смеси выполняется по методике Beattie – Whalley [23].

Расчет трехфазных течений

Расчет течения трехфазного продукта с газовой и двумя несмешивающимися жидкими фазами (например, нефть и вода) в настоящее время выполняется по методикам двухфазного газо-жидкостного течения. При этом считается, что две жидкие фазы образуют однородную жидкую эмульсию. Плотность такой эмульсии рассчитывается по однородной модели, а вязкость – по формуле Brinkman – Roscoe [40-41], обобщающей известную формулу Эйнштейна [42], с определением и учетом типа эмульсии ("вода в нефти" или "нефть в воде"). Точка инверсии фаз определяется из условия равенства величины вязкости (то есть когда вязкость эмульсии "вода в нефти" равна вязкости эмульсии "нефть в воде").

Предустановленные настройки методов расчета газожидкостных течений

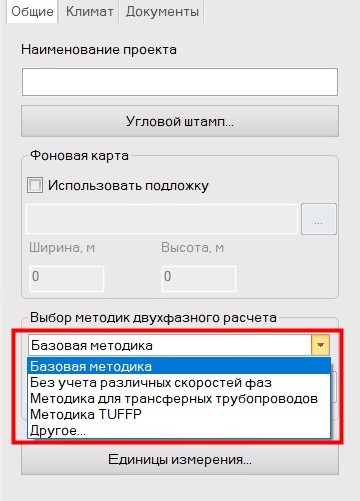
При установке вместе с программой поставляются следующие 4 варианта предустановленных профилей с методами расчета газожидкостных течений, доступных для выбора в общих данных по проекту:

Правила выбора методик каждого из указанных профилей содержатся в соответствующих XML файлах в директории установки программы (по умолчанию C:\Program Files (x86)\truboprovod\hst):

К ним относятся:

• "Базовая методика" (файл HST.xml) - в данном профиле прописаны методы расчета, имеющие наиболее широкую сферу применения:

• • расчет режима течения по методике Barnea;

  • расчет истинного газосодержания по методике Premoli;

  • расчет потерь на трение методами двухфазных мультипликаторов согласно рекомендациям Whalley:

  • • при малой массовой скорости потока и высоких величинах отношения вязкости жидкой фазы к вязкости газа - метод Локкарта-Мартинелли;

    • при высокой массовой скорости потока и высоких величинах отношения вязкости жидкой фазы к вязкости газа - метод Чисхолма;

    • при малых величинах отношения вязкости жидкой фазы к вязкости газа - метод Фриделя;

  • расчет потерь на местных сопротивлениях согласно рекомендациям [30].

• "Без учета различных скоростей фаз" (файл HST_HEM.xml) - те же методы, что и в "базовой" методике, но для расчета истинного газосодержания используется модель однородного течения (HEM).

• "Методика для трансферных трубопроводов" (файл HST-FR-BW, LOC -HEM.xml) - в данном профиле используются методы расчета, хорошо зарекомендовавшие себя при расчете "трансферных" трубопроводов (трубопроводов подачи нефти в парожидкостном состоянии из печей/подогревателей в ректификационную колонну):

• • расчет режима течения по методике Barnea;

  • расчет истинного газосодержания по методике Premoli;

  • расчет потерь на трение по методу Beattie – Whalley;

  • расчет потерь на местных сопротивлениях по модели однородного течения (HEM).

• "Методика TUFFP" (файл HST_Unified.xml)* - расчет режимов течений, истинного газосодержания и потерь на трение ведется по механистической модели Unified model (TUFFP). Расчет потерь на местных сопротивлениях при использовании данного профиля с настройками выполняется согласно рекомендациям [30]. При использовании методик механистической модели TUFFP Unified model "замыкающие соотношения" для данной модели (методы расчета коэффициента межфазного трения, истинных объемных содержаний фаз при снарядном течении, параметров уноса жидкости газом, длин промежутков между снарядами при снарядном течении и т. д.) задаются в настройках расчета трубопровода. Также при использовании методик TUFFP имеется возможность при возникновении перемежающихся (прерывистых) двухфазных течений прогнозировать их параметры – скорость движения газовых "снарядов", их частоту, длину межснарядной жидкой перемычки и т.д. Рассчитанные параметры можно затем экспортировать в программу СТАРТ-Проф для их учета в прочностном расчете трубопровода.

________________________________________________

* - Обратите внимание, что в некоторых случаях при использовании методик TUFFP возможны проблемы с определением режимов течения на вертикальных и наклонных участках трубопроводов. .

По умолчанию в расчетах используется "Базовая методика". Однако, при необходимости пользователь программы может как выбрать любой другой профиль с настройками, так и составить собственный XML-файл с желаемыми методами расчета двухфазного течения. Для загрузки собственного XML-файла с настройками необходимо в выпадающем списке выбора методов выбрать пункт "Другое", после чего в соответствующем поле (снизу от выпадающего списка с выбором методик) загрузить свой XML-файл с правилами выбора методов. Структура данного файла описана в следующем разделе.

Структура XML-файла с настройками выбора методов расчета газожидкостных течений

Как уже было упомянуто выше, настроить используемые методы расчета двухфазных течений в программе можно путем загрузки специального XML-файла, содержащего "правила выбора" методов расчета различных параметров двухфазного потока для различных элементов трубопровода при различных условиях (свойствах газовой и жидкой фазы, их расходов, скоростей и т.д.). К этим параметрам относятся:

• потери давления на трение (friction_losses)

• потери давления на местные сопротивления (local_losses)

• истинное газосодержание (void_fraction)

• режим течения (flow_pattern)

Общая схема данного файла приведена ниже:

<xs:schema

 xmlns:xs="http://www.w3.org/2001/XMLSchema">

 <xs:element name="friction_losses" type="method_type"/>

 <xs:element name="local_losses" type="method_type"/>

 <xs:element name="void_fraction" type="method_type"/>

 <xs:element name="flow_pattern" type="method_type"/>

</xs:schema>

Алгоритм выбора метода задается с помощью типа method_type, который определен следующим образом. Для каждого типа задается метод по умолчанию ("default") и несколько (возможно также одно или ни одного) условий выбора других методов (condition). Если ни одно из условий не подходит, то используется метод, заданный по умолчанию. Схема приведена ниже:

<xs:complexType name="method_type">

  <xs:sequence>

   <xs:element name="default"/>

   <xs:attribute name="method" type="xs:token"/>

   <xs:element name="condition" minOccurs=”0” maxOccurs=”unbounded”/>

   <xs:attribute name="method" type="xs:token"/>

   <xs:attribute name="pr" type="predicate_type”/>

  </xs:sequence>

 </xs:complexType>

В настоящее время в программе реализованы следующие методы расчета параметров паро-жидкостного течения (подробнее об этих методах и их применении см. выше):

Условия проверяются сверху вниз по файлу. Каждое условие выбора (condition) представляет собой проверку истинности некоторого предиката ("pr"). Если для какого-то условия значение соответствующего ему предиката истинно, то проверка прекращается и выбирается метод, соответствующий этому условию. Нижележащие условия в этом случае не проверяются.

Предикат является бинарной операцией, значениями которой могут быть только "ИСТИНА" или "ЛОЖЬ". Поддерживаются следующие типы логических операций:

• EQUAL – "ИСТИНА", если оба операнда равны между собой

• AND – "ИСТИНА", если значения обоих операндов истинны

• OR – "ИСТИНА", если значение хотя бы одного из операндов истинно

• GT – "ИСТИНА", если значение первого операнда больше значения второго. Значения операндов должны быть числовыми

• LT – "ИСТИНА", если значение первого операнда меньше значения второго. Значения операндов должны быть числовыми.

ХМL-схема предиката представлена ниже:

<xs:complexType name="predicat_type">

 <xs:element name="predicat"/>

 <xs:attribute name="name" type="xs:string"/>

 <xs:attribute name="expr1" type="expression_type”/>

 <xs:attribute name="operation" type="xs:token"/>

 <xs:attribute name="expr2" type="expression_type”/>

</xs: complexType >

Операнды предиката ("expr1" и "expr2") представляют собой арифметические выражения, внутри которых допустимы символы из множества +-*/(). Операндами арифметического выражения могут быть как переменные, так и константы или просто числа. В текущей версии программы допустимы следующие переменные:

• Visc_l – вязкость жидкой фазы, сСт

• Visc_g – вязкость газовой фазы, сСт

• G – массовая скорость потока (расход на единицу площади сечения), кг/м2с

• resistance_type – класс используемого гидравлического сопротивления. Значением этой переменной может быть либо число, которое определяется по первой колонке файла resistance.csv (расположенного в директории установки программы), либо одна из следующих констант:

• • Pipe – прямой участок трубы

  • Bend – отвод (независимо от его типа)

  • piping_component_type – гидравлическое сопротивление. Может принимать числовые значения из последней колонки файла resistance.csv (расположенного в директории установки программы), либо значения приведенных ниже символических констант:

  • • Orifice – диафрагма с острой кромкой

    • Confuser – конфузор

    • Sudden_contraction – внезапное сужение

    • Diffuser – диффузор

    • Abrupt_expansion – внезапное расширение

    • Knife_gate_valve – задвижка шиберная

    • Gate_valve – задвижка клиновая

    • Pinch_valve – задвижка с симметричным сужением проточной части

    • Ball_valve – шаровой кран

    • Straight_pipe_enter – вход в трубу

    • Straight_pipe_exit – выход из трубы

    • Butterfly_valve – затвор поворотный дисковый

    • Swing_check_valve - клапан обратный поворотный

    • Lift_check_valve - Клапан обратный подъемный

    • Forged_globe_valve - Клапан запорный штампованный

    • Globe_valve_type_rey - Клапан запорный фланцевый

    • Angle_valve - Клапан угловой

    • Control_valve - Регулирующий клапан

    • Flow_turn - Колено с острой кромкой без ниши

    • Flow_turn_in_tee - Колено с острой кромкой (тройник)

    • Z-type_flow_turn – Колено Z-образное

    • Expansion_joint - Компенсатор волнистый\\линзовый

    • U-type_expansion_loop - Компенсатор П-образный сварной

    • Tee_(side_leg) - Тройник в боковом ответвлении

    • Tee_(main_leg) – Тройник в проходе

    • Rise_(down) – Подъем/опуск

    • Component_with_known_change_of_pressure_and/or_temperature - Сопротивление с известным перепадом давления и/или температуры

    • Component_with_known_loss_coefficient - Сопротивление с известным коэффициентом сопротивления

    • Pump - насос

Список литературы

1. Azzopardy B.J. Gas-Liquid Flows. Begell House, Inc. N.Y., 2006.

2. Whalley P.B. Boiling, Condensation and Gas-Liquid Flow. Claredon Press, Oxford, 1987.

3. Yemada Taitel, A.E. Dukler. A Model for Predicting Flow Regime Transitions in Horizontal and Near Horizontal Gas-Liquid Flow. AIchE Journal, 1976, Vol. 22, No 1, pp.47-55.

4. D. Barnea. A Unified Model for Predicting Flow-Pattern Transitions for the Whole Range of Pipe Inclinations. Int. J. Multiphase Flow, 1987,  Vol.13, No 1, pp. 1-12.

5. Petalas N., Aziz K. A Mechanistic Model for Stabilized Multiphase Flow in Pipes. Technical Report for Members of the Reservoir Simulation Industrial Affiliates Program (SUPRI-B) and Horizontal Well Industrial Affiliates Program (SUPRI-HW), Stanford University, CA, 1997.

6. Chen Y. Modeling Gas-Liquid Flow in Pipes: Flow Pattern Transitions and Drift-Flux Modeling. Master of Science Degree Thesis. Stanford University. 2001.

7. Zivi S.M. Estimation of Steady-State Steam Void-Fraction by Means of the Principle of Minimum Entropy Generation. J. Heat Transfer, 1964, Vol. 86, pp. 247-252.

8. Fauske H. Critical Two-Phase, Steam-Water Flows. In: Proc. Of Heat Transfer and Fluid Mechanics Institute. 1961, Stanford University Press, Stanford, CA, pp. 79–89.

9. Thom J.R.S. Prediction of Pressure Drop during Forced Circulation Boiling of Water. Int. J. Heat Mass Transfer, 1964, Vol. 7, pp. 709-724.

10. Baroczy C.J. A systemic correlation for two phase pressure drop.  1966. Chem. Eng. Progr. Symp. Ser. 62, pp. 232–249.

11. Turner J.M., Wallis G.B. The separate-cylinders model of two-phase flow. Paper No. NYO-3114-6. Thayer’s School Eng., Dartmouth College, Hanover, NH, USA. 1965.

12. Lockhart R.W., Martinelli R.C. Proposed Correlation of Data for Isothermal Two-Phase, Two Component Flow in Pipes. Chem. Eng. Progr.,  1949, Vol. 45, pp. 39–48.

13. Д. Чисхолм. Двухфазные течения в трубопроводах и теплообменниках: Пер. с англ. Москва, «Недра», 1986. 204 с.

14. Smith S.L. Void Fractions in Two phase Flow: a Correlation based upon an Equal Velocity Head Model. Proc. Inst. Mech. Engrs., 1969, Vol. 184, No 36, pp. 647-657.

15. Premoli A., Francesco D., Prima A. An Empirical Correlation for Evaluating Two-Phase Mixture Density under Adiabatic Conditions. Paper B9. In: European Two-Phase Flow Group Meeting, Milan, Italy. 1970.

16. Zuber N., Findlay J.A. Average volumetric concentration in two-phase flow systems. J. Heat Transfer, 1965, Vol. 87, pp. 435–468.

17. Rouhani S.Z., Axelsson E. Calculation of void volume fraction in the sub cooled and quality boiling regions. Int. J. Heat Mass Transfer, 1970, Vol. 13, pp. 383–393.

18. Rouhani S.Z. Modified Correlations for Void and Two-Phase Pressure Drop. AE-RTV-851. 1969.

19. D. Steiner, Heat Transfer to Boiling Saturated Liquids, in: VDI-War meatlas (VDI Heat Atlas), Chapter Hbb, VDI-Gessellschaft Verfahrenstechnik und Chemieingenieurwesen (GCV), Dusseldorf, 1993.

20. Dix G.E. Vapor Void Fraction for Forced Convection with Boiling and Low Flow Rates. PhD Thesis, Univ. of California, Berkeley, 1971.

21. Ghajar A.J., Woldesemayat M.A. Comparison of Void Fraction Correlations for Different Flow Patterns in Horizontal and Upward Inclined Pipes. Int. J. Multiphase Flow. 2007, Vol. 33, pp. 347-370.

22. H. Goda, T. Hibiki, S. Kim, M. Ishii, J. Uhle. Drift-Flux Model for Downward Two-Phase Flow. Int. J. Heat and Mass Transfer. 2003, Vol. 46, pp. 4835-4844.

23. Beattie D.R.H., Whalley P.B. A Simple Two-Phase Frictional Pressure Drop Calculation Method. Int. J. Multiphase Flow. 1982, Vol. 8, No 1, pp. 83-87.

24. Shannak B.A. Frictional Pressure Drop of Gas Liquid Thow-Phase Flow in Pipes. Nuclear Engineering and Design, 2008, Vol. 238, pp. 3277-3284.

25. Friedel L. Improved Friction Pressure Drop Correlations for Horizontal and Vertical Tow-Phase Pipe Flow. Presented at European Two-phase Flow Group Meeting, Ispra, Italy. Paper E2, June 1979.

26. Muller-Steinhagen H., Heck K. A Simple Pressure Drop Correlation for Two-Phase Flow in Pipes. Chem. Eng. Process., 1986, Vol. 20, pp. 297-308.

27. IHS ESDU 01014. Frictional Pressure Gradient in Adiabatic Flows of Gas-Liquid Mixtures in Horizontal Pipes: Prediction Using Empirical Correlations and Database. 2002.

28. Simpson H.C., Rooney D.H., Grattan E. Two-Phase Flow through Gate Valves and Orifice Plates. Paper E2. International Conference Physical Modelling of Multi-phase Flow. Coventry, England. 1983.

29. Morris S.D. Two-phase Pressure Drop across Valves and Orifice Plates. Paper E2. European Two-phase Flow Group Meeting. Marchwood Engng Lab., Marchwood, Southampton, England, 1985.

30. IHS ESDU 89012. Two-Phase Flow Pressure Losses in Pipeline Fittings. 2007.

31. Миркин А.З., Усиньш В.В. Трубопроводные системы. Справочное издание. М., Химия, 1991. 256 с.

32. Bendiksen, K., Malnes, D., Moe, R., Nuland, S., “The Dynamic Two-Fluid Model OLGA, Theory and Application”, SPE Production Engineering, 1991.

33. Bøe, A., “Severe slugging characteristics: (1) Flow regime for severe slugging (2) Point model simulation study”, Presented at Selected Topics in Two-Phase Flow, NTH, Trondheim, Norway, 1981.

34. Kajero, O., Azzopardi, B., Abdulkareem., L, “Experimental investigation of the effect of liquid viscosity on slug flow in small diameter bubble column”, EPJ Web of Conferences 25, 01037, 2012.

35. Malekzadeh, R., “Severe slugging in gas-liquid two-phase pipe flow”, PhD dissertation, TU Delft, 2012.

36. Nuland, S., Malvik, I.M., Valle, A., Hende, P., “Gas fractions in slugs in dense-gas two-phase flow from horizontal to 60 degrees of inclination”. The 1997 ASME Fluids Engineering Division Summer, 1997.

37. Schmidt, Z., Doty, D., Kunal., D.R., “Severe Slugging in Offshore Pipeline Riser-Pipe Systems”, SPE-12334-PA, 1985.

38. Taitel, Y., “Stability of severe slugging,” International Journal of Multiphase Flow, vol. 12, no. 2, pp. 203 – 217, 1986.

39. Xiaoming, L., Limin, H., Huawei, M. “Flow Pattern and Pressure Fluctuation of Severe Slugging in Pipeline-riser System”, Chinese Journal of Chemical Engineering, 19(1) 26—32, 2011.

40. Brinkman, H. C. (1952). The viscosity of concentrated suspensions and solutions. J. of Chem. Phy., 20(4): 571.

41. Roscoe, R. (1952). The viscosity of suspensions of rigid spheres. British journal of applied physics, 267-269.

42. Einstein, A. (1906). Eine neue bestimmung der moleküledimensionen, Annalen Phys., 19: 289-306

43. Hong-Quan Zhang, Qian Wang, Cem Sarica, James P. Brill. Unified Model for Gas-Liquid Pipe Flow via Slug Dynamics – Part 1: Model Development. Trans. of ASME, 2003, Vol. 125, pp. 266-273.

44. Hong-Quan Zhang, Qian Wang, Cem Sarica, James P. Brill. Unified Model for Gas-Liquid Pipe Flow via Slug Dynamics – Part 2: Model Validation. Trans. of ASME, 2003, Vol. 125, pp. 274-283.

45. Hong-Quan Zhang, Qian Wang, James P. Brill. A Unified Mechanistic Model for Slug Liquid Holdup and Transition between Slug and Disperse Bubble Flows. Int. J. Multiphase Flow, Vol. 29, pp. 97-107.

46. Hong-Quan Zhang, Cem Sarica. A Model of Wetted-Wall Fraction and Gravity Center of Liquid Film in Gas/Liquid Pipe Flow. SPE Journal, 2011, Vol. 16, N 3, pp. 692-697.

47. Cohen L.S., Hanratty T.J. Effect of Waves at a Gas-Liquid Interface on a Turbulent Air Flow. J. Fluid Mech. 1968, Vol. 31, N 3, pp. 467-479.