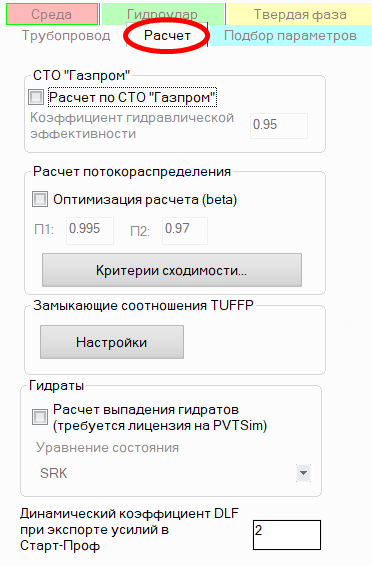
Дополнительные настройки расчета трубопровода
На вкладке "Расчет" Окна параметров объекта для трубопровода можно также указать некоторые "тонкие" настройки расчета и дополнительные опции, которые могут потребоваться в отдельных нечастых случаях.

К ним относятся:
Расчет по СТО "Газпром" 2-3.5-051-2006 - данная опция предназначена для уточненного расчета магистральных газопроводов (с давлением природного газа от 1.18 до 15МПа и диаметрами до DN1400 включительно). При включении данной опции программа переключается с расчетов по универсальным методикам (применимым для любых продуктов в трубопроводах любого типа) на специализированные методики, предназначенные исключительно для расчетов природного газа в магистральных газопроводах. При включении данной опции необходимо ввести значение коэффициента гидравлической эффективности в соответствующее поле, а также указать некоторые дополнительные параметры теплового взаимодействия трубопровода с окружающей средой. Также обратите внимание, что при включении опции Расчет по СТО "Газпром" метод расчета свойств продукта автоматически переключается на библиотеку "Свойства", так как только расчетные методики данной библиотеки в точности соответствуют требованиям СТО Газпром 2-3.5-051-2006.
Оптимизация расчета потокораспределения в сложных схемах - эта опция используется для расчетов сложных трубопроводных систем с большим числом разветвлений, в которых встречаются несоразмерные по величинам расходы продукта (когда расходы в некоторых ветвях в сотни или тысячи раз меньше, чем в других). Использование этой опции в отдельных случаях позволяет обеспечить лучшую сходимость расчетов таких трубопроводов.
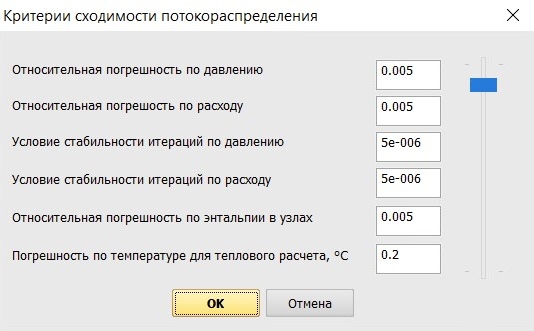
Критерии сходимости – эта опция позволяет установить погрешности (по давлению, расходу и т.д.) расчета. Погрешности можно как задавать вручную для каждого параметра, так и менять синхронно для всех параметров перемещая вверх-вниз соответствующий "ползунок" (вверху наиболее точный расчет с наименьшими погрешностями, внизу - максимальные погрешности). Увеличение погрешностей позволяет обеспечить лучшую сходимость расчетов трубопроводов с высокими расходами и скоростями потоков, а также с несоразмерными величинами расходов в различных ветвях (к примеру, когда на некоторых ветвях трубопровода расходы на несколько порядков меньше, чем на других).
Замыкающие соотношения TUFFP - эта опция позволяет более гибко настроить так называемые "замыкающие соотношения" для гидравлического расчет двухфазного течения по методике "Unified model" проекта TUFFP.
К "замыкающим соотношениям" относятся методы расчетов определенных параметров двухфазного потока: коэффициента межфазного трения, истинных объемных содержаний фаз при снарядном течении, параметров уноса жидкости газом, длин промежутков между снарядами при снарядном течении и т. д.:
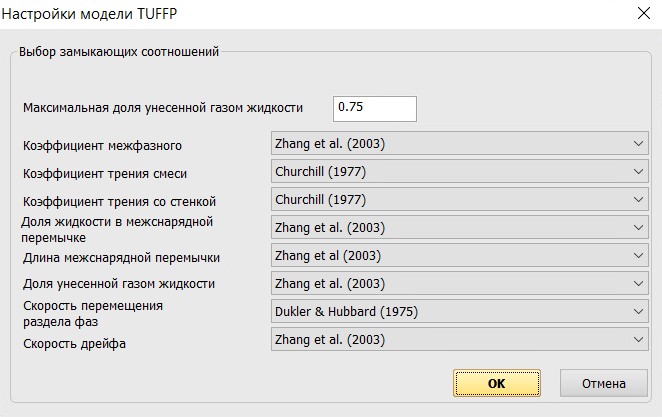
По умолчанию смачиваемая поверхность и форма межфазной поверхности при расслоенном течении рассчитывается согласно [3], истинные объемные содержания фаз при снарядном течении и параметры уноса жидкости газом согласно [1-2], длина промежутка между снарядами при снарядном течении согласно [5-6], коэффициент межфазного трения согласно [4]. Для расчета коэффициента гидравлического трения используется универсальная формула Черчилля [7].
Обратите внимание, что для использования модели "Unified model" необходимо при задании методов расчета двухфазного течения выбрать "Методику TUFFP". Более подробно методики, использующиеся в расчетах по «Unified model» описаны в [8-12].
Расчет выпадения гидратов - данная опция позволяет выполнять расчет выпадения гидратов по ходу течения продукта в трубопроводе с использованием специального термодинамического пакета PVTSim производства Calsep. Для использования данной опции пакет PVTSim должен быть установлен на данном компьютере и должна быть доступна лицензия на него. Методики расчета выпадения гидратов подробно описаны в документации к PVTSim.
Динамический коэффициент DLF при экспорте усилий в СТАРТ-Проф - данный коэффициент используется при расчете усилий, возникающих при гидравлическом ударе и при снарядном режиме газожидкостного течения в трубопроводах, значения которых экспортируются в программу "СТАРТ-Проф" для прочностного анализа трубопровода. Он позволяет учесть, что при приложении к трубопроводной системе динамических нагрузок (вызванных гидроударом или снарядным течением) деформации конструкции могут оказаться больше деформаций от статических нагрузок в 1.0-2.0 раза. Поскольку расчет в "СТАРТ-Проф" на нагрузки от снарядного течения и гидроудара выполняется статическим методом, то для учета динамического характера приложения нагрузки рекомендуется вводить худшее значение динамического коэффициента DLF=2.0. Рассчитанные программой усилия будут домножаться на коэффициент DLF, и полученные значения будут переданы в "СТАРТ-Проф".
Список литературы
1. Hong-Quan Zhang, Qian Wang, Cem Sarica, James P. Brill. Unified Model for Gas-Liquid Pipe Flow via Slug Dynamics – Part 1: Model Development. Trans. of ASME, 2003, Vol. 125, pp. 266-273.
2. Hong-Quan Zhang, Qian Wang, James P. Brill. A Unified Mechanistic Model for Slug Liquid Holdup and Transition between Slug and Disperse Bubble Flows. Int. J. Multiphase Flow, Vol. 29, pp. 97-107.
3. Hong-Quan Zhang, Cem Sarica. A Model of Wetted-Wall Fraction and Gravity Center of Liquid Film in Gas/Liquid Pipe Flow. SPE Journal, 2011, Vol. 16, N 3, pp. 692-697.
4. Cohen L.S., Hanratty T.J. Effect of Waves at a Gas-Liquid Interface on a Turbulent Air Flow. J. Fluid Mech. 1968, Vol. 31, N 3, pp. 467-479.
5. Taitel Y., Barnea D., Dukler A.E. Modeling Flow Pattern Transitions for Steady Upward Gas-Liquid Flow in Vertical Tubes. AIChE Journal. 1981, Vol. 26, N 3, pp. 345-354.
6. Barnea D., Brauner N. Holdup of the Liquid Slug in Two-Phase Intermitted Flow. Int. J. Multiphase Flow. 1985, Vol. 11, N 1, pp. 43-49.
7. Churchill S.W. Friction Factor Equations Spans all Fluid-Flow Regimes.Chem. Eng. 1977, Vol. 7, pp. 91-92.91. Bendiksen, K., Malnes, D., Moe, R., N
8. Hong-Quan Zhang, Qian Wang, Cem Sarica, James P. Brill. Unified Model for Gas-Liquid Pipe Flow via Slug Dynamics – Part 1: Model Development. Trans. of ASME, 2003, Vol. 125, pp. 266-273.
9. Hong-Quan Zhang, Qian Wang, Cem Sarica, James P. Brill. Unified Model for Gas-Liquid Pipe Flow via Slug Dynamics – Part 2: Model Validation. Trans. of ASME, 2003, Vol. 125, pp. 274-283.
10. Hong-Quan Zhang, Qian Wang, James P. Brill. A Unified Mechanistic Model for Slug Liquid Holdup and Transition between Slug and Disperse Bubble Flows. Int. J. Multiphase Flow, Vol. 29, pp. 97-107.
11. Hong-Quan Zhang, Cem Sarica. A Model of Wetted-Wall Fraction and Gravity Center of Liquid Film in Gas/Liquid Pipe Flow. SPE Journal, 2011, Vol. 16, N 3, pp. 692-697.
12. Cohen L.S., Hanratty T.J. Effect of Waves at a Gas-Liquid Interface on a Turbulent Air Flow. J. Fluid Mech. 1968, Vol. 31, N 3, pp. 467-479.