

 |
Штуцер-МКЭ 3.5. Руководство пользователя |  |
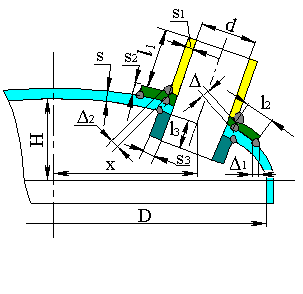
Расчетная схема врезки штуцера в сферическую оболочку приведена на рисунке 5.35.
 |
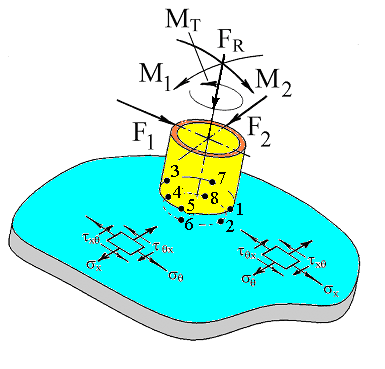 |
| Рис. 5.35. Расчетная схема соединения штуцера со стенкой сосуда | |
Расчетная схема врезки штуцера в сферическую оболочку может также использоваться при определении прочности и жесткости врезки штуцера в эллиптическое днище.
При этом для определения $R_m$ вместо диаметра $D$ используется расчетный диаметр для эллиптических днищ:
| $$ D_{p} = \frac{D^2}{2H}\sqrt{1-4\frac{D^2-4H^2}{D^4}x^2}. $$ | (5.60) |
При определении напряжений в сферической оболочке используются относительные безразмерные усилия и моменты, которые зависят от геометрических параметров оболочки и патрубка $U$, $\gamma$ и $\rho$.
Безразмерные геометрические параметры:
| $$ U = \frac{r_0}{\sqrt{R_m(s-c)}}, $$ | (5.61) |
| $$ \gamma = \frac{r_m}{\sqrt{R_m(s_1-c_s)}}, $$ | (5.62) |
| $$ \rho = \frac{s-c}{s_1-c_s}, $$ | (5.63) |
где $r_m = 0.5(d+s_1+c_s)$ - средний радиус патрубка.
Относительные безразмерные усилия и моменты в тангенсальном ($\theta$) направлении:
| $n_{\theta F}$ | - | мембранное усилие от действия $F_R$ |
| $m_{\theta F}$ | - | изгибающий момент от действия $F_R$ |
| $n_{\theta M}$ | - | мембранное усилие от действия $M_{1(2)}$; |
| $m_{\theta M}$ | - | изгибающий момент от действия $M_{1(2)}$. |
Относительные безразмерные усилия и моменты радиальном ($X$) направлении:
| $n_{RF}$ | - | мембранное усилие от действия $F_R$ |
| $m_{RF}$ | - | изгибающий момент от действия $F_R$ |
| $n_{RM}$ | - | мембранное усилие от действия $M_{1(2)}$; |
| $m_{RM}$ | - | изгибающий момент от действия $M_{1(2)}$. |
Тангенсальные мембранные напряжения от силы $F_R$:
| $$ \sigma_{m\theta}(F_R) = n_{\theta F} \frac{F_R}{R_m(s-c)}, $$ | (5.64) |
где $n_{\theta F}$ определяется по [14].
Тангенсальные изгибные напряжения от силы $F_R$:
| $$ \sigma_{b\theta}(F_R) = m_{\theta F} \frac{6F_R}{(s-c)^2}, $$ | (5.65) |
где $m_{\theta F}$ определяется по [14].
Радиальные мембранные напряжения от силы $F_R$:
| $$ \sigma_{mx}(F_R) = n_{RF} \frac{F_R}{(s-c)^2}, $$ | (5.66) |
где $n_{RF}$ определяется по [14].
Радиальные изгибные напряжения от силы $F_R$:
| $$ \sigma_{bR}(F_R) = m_{RF} \frac{6F_R}{(s-c)^2}, $$ | (5.67) |
где $m_{RF}$ определяется по [14].
Тангенсальные мембранные напряжения в расчетных точках 5-8 от момента $M_1$ и в точках 1-4 от момента $M_2$:
| $$ \sigma_{m\theta}(M) = n_{\theta M} \frac{M}{(s-c)^2\sqrt{R_m(s-c)}}, $$ | (5.68) |
где $n_{\theta M}$ определяется по [14].
Тангенсальные изгибные напряжения от момента $M_1$ в точках 5-8 и от момента $M_2$ в точках 1-4:
| $$ \sigma_{b\theta}(M) = m_{\theta M} \frac{6M}{(s-c)^2\sqrt{R_m(s-c)}}, $$ | (5.69) |
где $m_{\theta M}$ определяется по [14].
Радиальные мембранные напряжения от момента $M_1$ в точках 5-8 и от момента $M_2$ в точках 1-4:
| $$ \sigma_{mR}(M) = n_{RM} \frac{M}{(s-c)^2\sqrt{R_m s}}, $$ | (5.70) |
где $n_{RM}$ определяется по [14].
Радиальные изгибные напряжения от момента $M_1$ в точках 5-8 и от момента $M_2$ в точках 1-4:
| $$ \sigma_{bR}(M) = m_{RM} \frac{6M}{(s-c)^2\sqrt{R_m s}}, $$ | (5.71) |
где $m_{RM}$ определяется по [14].
От крутящего момента в соединении штуцера и обечайки возникают касательные напряжения:
| $$ \tau_{\theta x} = \frac{M_T}{2\pi r^2_0 (s-c)}. $$ | (5.72) |
Силы $F_1$ в точках 5-8 и $F_2$ в точках 1-4 создают мембранные сдвиговые напряжения:
| $$ \tau_{x \theta} = \frac{F_{1(2)}}{\pi r_0 (s-c)}. $$ | (5.73) |
Местные мембранные напряжения от внутреннего давления определяются в зависимости от коэффициента интенсификации напряжения, полученного для поперечного сечения обечайки $I_{\theta p} = I_{xp}$ (рис. 5.35).
Окружное напряжение от внутреннего давления во всех расчетных точках:
| $$ \sigma_{\theta p} = p I_{\theta p} \frac{D+(s+s_2-c)}{2(s+s_2-c)}, $$ | (5.74) |
Продольное (радиальное) напряжение от внутреннего давления во всех расчетных точках определяется по формуле 5.74 при $I_{\theta p} = 1$.
Если расчетный коэффициент $I_{\theta p} < 1$, то для определения окружных и осевых напряжений во всех расчетных точках врезки используется коэффициент интенсификации равный $0.5(1+I_{\theta p})$.
В общем случае, все приложенные нагрузки на штуцер можно разложить по трем направлениям, т.е. представить как одновременно действующие силы $F_R$, $F_1$, $F_2$, и моменты $M_1$, $M_2$, $M_T$. После определения напряжений от действующих сил и давления, суммарные напряжения в расчетных точках (1-8) определяются с учетом знаков согласно таблице 5.16.
При наличии коррозионно-активной сероводородсодержащей среды выполняется дополнительный расчет растягивающих напряжений на внутренних поверхностях обечайки (точки 2, 4, 6, 8):
| $$ \sigma_{in} = \max{\left\{ \frac{1}{2} \left( \sigma_{\theta}+\sigma_x+\sqrt{(\sigma_{\theta}-\sigma_x)^2+4\tau^2_{\theta x}} \right); 0 \right\}}. $$ | (5.75) |
| Таблица 5.16. Местные напряжения в сферической оболочке в зоне врезки штуцера, работающего под действием внутреннего давления и внешних нагрузок согласно WRC 107 | ||||||||
| Окружные (отн. патр.) напряжения, $\sigma_{\theta}$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Мембранные от $F_R$ | - | - | - | - | - | - | - | - |
| Изгибные от $F_R$ | - | + | - | + | - | + | - | + |
| Мембранные от $M_1$ | - | - | + | + | ||||
| Изгибные от $M_1$ | - | + | + | - | ||||
| Мембранные от $M_2$ | - | - | + | + | ||||
| Изгибные от $M_2$ | - | + | + | - | ||||
| Окружные напряжения от давления $\sigma_{\theta p}$ | + | + | + | + | + | + | + | + |
| Суммарные мембранные окружные напряжения $\sigma_{m\theta}$ | ||||||||
| Суммарные окружные напряжения $\sigma_{\theta}$ (форм. 5.3.1) | ||||||||
| Радиальные (отн. патр.) напряжения, $\sigma_x$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Мембранные от $F_R$ | - | - | - | - | - | - | - | - |
| Изгибные от $F_R$ | - | + | - | + | - | + | - | + |
| Мембранные от $M_1$ | - | - | + | + | ||||
| Изгибные от $M_1$ | - | + | + | - | ||||
| Мембранные от $M_2$ | - | - | + | + | ||||
| Изгибные от $M_2$ | - | + | + | - | ||||
| Радиальные напряжения от давления $\sigma_{xp}$ | + | + | + | + | + | + | + | + |
| Суммарные мембранные продольные напряжения $\sigma_{mx}$ | ||||||||
| Суммарные продольные напряжения $\sigma_{x}$ (форм. 5.3.1) | ||||||||
| Сдвиговые напряжения от $M_t$ | + | + | + | + | + | + | + | + |
| Сдвиговые напряжения от $F_1$ | - | - | + | + | ||||
| Сдвиговые напряжения от $F_2$ | + | + | - | - | ||||
| Суммарные сдвиговые напряжения $\tau_{\theta x}$ | ||||||||
| Приведенные общие напряжения $\sigma_{экв}$ | ||||||||
| Растягивающие напряжения на внутренней поверхности $\sigma_{in}$ | ||||||||

Штуцер-МКЭ 3.5. Руководство пользователя
Copyright © 2003-2025, НТП Трубопровод