

 |
Штуцер-МКЭ 3.5. Руководство пользователя |  |
При определении напряжений в цилиндрической обечайке используются относительные безразмерные усилия и моменты, которые зависят от геометрических параметров обечайки $\gamma = \displaystyle\frac{R_m}{(s-c)}$ и штуцера $\beta = \displaystyle\frac{0.875 r_0}{R_m}$ [14], где $R_m = \displaystyle\frac{(D+s+c)}{2}$ - средний радиус обечайки; $r_0 = \displaystyle\frac{d+2s_1}{2}$ - внешний радиус патрубка штуцера.
Относительные безразмерные усилия и моменты в окружном направлении:
| $n_{\theta F}$ | - | мембранное усилие от действия $F_R$ |
| $m_{\theta F}$ | - | изгибающий момент от действия $F_R$ |
| $n_{\theta MC}$ | - | мембранное усилие от действия $M_C$; |
| $m_{\theta MC}$ | - | изгибающий момент от действия $M_C$ |
| $n_{\theta ML}$ | - | мембранное усилие от действия $M_L$; |
| $m_{\theta ML}$ | - | изгибающий момент от действия $M_L$. |
Относительные безразмерные усилия и моменты в продольном направлении:
| $n_{\theta XF}$ | - | мембранное усилие от действия $F_R$ |
| $m_{\theta XF}$ | - | изгибающий момент от действия $F_R$ |
| $n_{\theta XMC}$ | - | мембранное усилие от действия $M_C$; |
| $m_{\theta XMC}$ | - | изгибающий момент от действия $M_C$ |
| $n_{\theta XML}$ | - | мембранное усилие от действия $M_L$; |
| $m_{\theta XML}$ | - | изгибающий момент от действия $M_L$. |
Окружные мембранные напряжения от силы $F_R$:
| $$ \sigma_{m\theta}(F_R) = n_{\theta F} \frac{F_R}{R_m(s-c)}, $$ | (5.33) |
где $n_{\theta F}$ определяется по [14] (для расчетных точек (1-4) в продольном сечении определяется по рис.7.1, а для расчетных точек (5-8) в поперечном сечении по рис.7.2).
Окружные изгибные напряжения от силы $F_R$:
| $$ \sigma_{b\theta}(F_R) = m_{\theta F} \frac{6F_R}{(s-c)^2}, $$ | (5.34) |
где $m_{\theta F}$ определяется по [14] (в продольном (т.1-4) и поперечном (т.5-8) сечении определяется по рис.7.3 и 7.4 соответственно).
Продольные мембранные напряжения от силы $F_R$:
| $$ \sigma_{mx}(F_R) = n_{XF} \frac{F_R}{R_m(s-c)}, $$ | (5.35) |
где $n_{XF}$ определяется по [14] (определяется в продольном (т.1-4) и поперечном (т.5-8) сечении по рис.7.2 и 7.1 соответственно).
Продольные изгибные напряжения от силы $F_R$:
| $$ \sigma_{bx}(F_R) = m_{XF} \frac{6F_R}{(s-c)^2}, $$ | (5.36) |
где $m_{XF}$ определяется по [14] (определяется в продольном (т.1-4) и поперечном (т.5-8) сечении по рис.7.5 или 7.6 соответственно).
Окружные мембранные напряжения от момента $M_C$:
| $$ \sigma_{m\theta}(M_C) = n_{\theta MC} \frac{M_C}{R^2_m\beta(s-c)}, $$ | (5.37) |
где $n_{\theta MC}$ определяется по [14] (определяется в поперечном сечении (т.5-8) по рис.7.7).
Окружные изгибные напряжения от момента $M_C$:
| $$ \sigma_{b\theta}(M_C) = m_{\theta MC} \frac{6M_C}{R_m\beta(s-c)^2}, $$ | (5.38) |
где $m_{\theta MC}$ определяется по [14] (определяется в поперечном сечении (т.5-8) по рис.7.8).
Продольные мембранные напряжения от момента $M_C$:
| $$ \sigma_{mx}(M_C) = n_{XMC} \frac{M_C}{R^2_m\beta(s-c)}, $$ | (5.39) |
где $n_{XMC}$ определяется по [14] (определяется в поперечном сечении (т.5-8) по рис.7.9).
Продольные изгибные напряжения от момента $M_C$:
| $$ \sigma_{bx}(M_C) = m_{XMC} \frac{6M_C}{R_m\beta(s-c)^2}, $$ | (5.40) |
где $m_{XMC}$ определяется по [14] (определяется в поперечном сечении (т.5-8) по рис.7.10).
Окружные мембранные напряжения от момента $M_L$:
| $$ \sigma_{m\theta}(M_L) = n_{\theta ML} \frac{M_L}{R^2_m\beta(s-c)}, $$ | (5.41) |
где $n_{\theta ML}$ определяется по [14] (определяется в продольном сечении (т.1-4) по рис.7.11).
Окружные изгибные напряжения от момента $M_L$:
| $$ \sigma_{b\theta}(M_L) = m_{\theta ML} \frac{6M_L}{R_m\beta(s-c)^2}, $$ | (5.42) |
где $m_{\theta ML}$ определяется по [14] (определяется в продольном сечении (т.1-4) сечении по рис.7.12).
Продольные мембранные напряжения от момента $M_L$:
| $$ \sigma_{mx}(M_L) = n_{XML} \frac{M_L}{R^2_m\beta(s-c)}, $$ | (5.43) |
где $n_{XML}$ определяется по [14] (определяется в продольном сечении (т.1-4) по рис.7.13).
Продольные изгибные напряжения от момента $M_L$:
| $$ \sigma_{bx}(M_L) = m_{XML} \frac{6M_L}{R_m\beta(s-c)^2}, $$ | (5.44) |
где $m_{XML}$ определяется по [14] (определяется в продольном сечении (т.1-4) по рис.7.14).
От крутящего момента в соединении штуцера и обечайки возникают касательные напряжения:
| $$ \tau_{\theta x} = \frac{M_T}{2 \pi r^2_0 (s-c)}. $$ | (5.45) |
Силы $F_C$ и $F_L$ создают мембранные сдвиговые напряжения в продольном (т.1-4) и окружном (т.5-8) сечении соответственно:
| $$ \tau_{x\theta} = \frac{F_C}{\pi r_0 (s-c)}, $$ | (5.46) |
| $$ \tau_{\theta x} = \frac{F_L}{\pi r_0 (s-c)}. $$ | (5.47) |
Предложенный метод основан на двух допущениях [19]:
| 1) | Средние значения напряжений в расчетной зоне укрепления отверстия $\sigma_{\theta(x)cp}$ определяются из отношений силы давления к площади поперечного сечения в пределах расчетной области. |
| 2) | Мембранные напряжения имеют линейное распределение вдоль зоны укрепления отверстия (рис. 5.32), где |
| $\sigma_{\theta(x)0}$ | - | напряжения в обечайке вне расчетной зоны; |
| $\sigma_{\theta(x)ср}$ | - | средние напряжения в середине расчетной зоны укрепления отверстия; |
| $\sigma_{\theta(x)р}$ | - | местные мембранные напряжения в расчетных точках сопряжения штуцера и обечайки. |
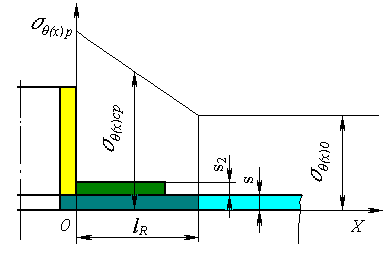 |
| Рис. 5.32. Распределение напряжений в расчетной зоне штуцера |
Мембранные напряжения в расчетных точках:
| $$ \sigma_{\theta(x)p} = 2\sigma_{\theta(x)cp} - \sigma_{\theta(x)0}. $$ | (5.48) |
Местное мембранное окружное напряжение от внутреннего давления в зоне врезки штуцера можно представить в виде:
| $$ \sigma_{\theta p} = p I_{\theta p} \frac{D+(s+s_2-c)}{2(s+s_2-c)}, $$ | (5.49) |
где $I_{\theta p}$ - коэффициент интенсификации напряжения от давления в продольном сечении обечайки (т.1-4, рис. 5.31). Для поперечного сечения (т.5-8, рис. 5.31) $I_{\theta p} = 1$.
Расчетная схема для определения коэффициента интенсификации в продольном сечении представлена на рис. 5.33:
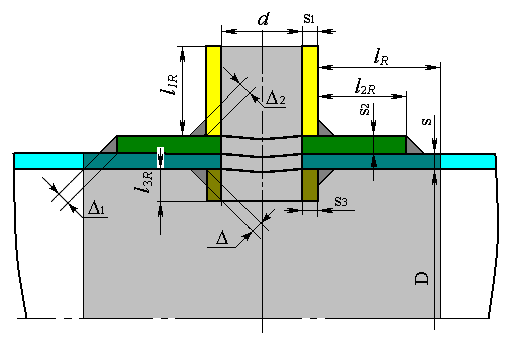 |
| Рис. 5.33. Расчетная схема штуцера в продольном сечении обечайки |
Коэффициент интенсификации напряжений от внутреннего давления в продольном сечении:
| $$ I_{\theta p} = \frac{2 (s+s_2-c)\left[ (d+2c_s)(l_{1R}-c) + (D+2c)(l_{R}+s_1+0.5d) \right]} {\left( D+(s+s_2-c) \right) \left[ l_R(s-c)+l_{1R}(s_1-c_s)+l_{2R}s_2+l_{3R}(s_3-2c_s)+(\Delta^2+\Delta^2_1+\Delta^2_2) \right]} - 1, $$ | (5.50) |
где расчетная длина обечайки:
| $$ l_{R} = \left\{ \begin{array}{lll} \min{\left\{ 8(s-c); \sqrt{2D(s-c)} \right\}}, & s_2 < 0.5(s-c), & \\ \min{\left\{ 10(s-c); \sqrt{2D(s-c)} \right\}}, & s_2 > 0.5(s-c), & l_2 \ge 2(s-c), \\ \min{\left\{ 8(s+s_2-c); \sqrt{2D(s-c)} \right\}}, & s_2 > 0.5(s-c), & l_2 \ge 2(s+s_2-c); \\ \end{array} \right. $$ | (5.51) |
расчетная длина внешней части штуцера:
| $$ l_{1R} = \min{\left\{ 8(s-c); s+s_2-c+0.55\sqrt{d(s_1-c_s)}+0.5\Delta_2 \right\}}; $$ | (5.52) |
расчетная длина накладного листа:
| $$ l_{2R} = \min{\left\{ l_2; l_R \right\}}; $$ | (5.53) |
расчетная длина внутренней части штуцера:
| $$ l_{3R} = \min{\left\{ l_3; 8(s+s_2-c); 0.55\sqrt{d(s_3-c_s)}+0.5\Delta \right\}}. $$ | (5.54) |
Местное мембранное продольное напряжение от внутреннего давления:
| $$ \sigma_{xp} = p I_{xp} \frac{D+(s+s_2-c)}{4(s+s_2-c)}. $$ | (5.55) |
Расчетная схема для определения коэффициента интенсификации в поперечном сечении представлена на рис. 5.34:
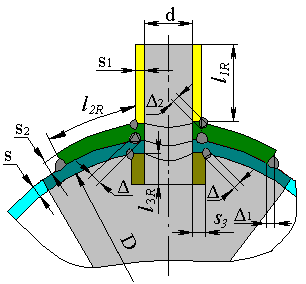 |
| Рис. 5.34. Расчетная схема штуцера в поперечном сечении обечайки |
Коэффициент интенсификации напряжений от внутреннего давления в поперечном сечении:
| $$ I_{xp} = \frac{2 (s+s_2-c)\left[ 2(d+2c_s)(l_{1R}-c) + (D+2c)(l_{R}+s_1+0.5d) \right]} {\left( D+(s+s_2-c) \right) \left[ l_R(s-c)+l_{1R}(s_1-c_s)+l_{2R}s_2+l_{3R}(s_3-2c_s)+(\Delta^2+\Delta^2_1+\Delta^2_2) \right]} - 1, $$ | (5.56) |
Для продольного сечения (т.1-4) $I_{xp} = 1$.
Если расчетные коэффициенты $I_{\theta(x)p} < 1$, то для определения окружных и продольных напряжений во всех расчетных точках врезки используются следующие выражения:
| $$ \sigma_{\theta p} = p \frac{1+I_{\theta p}}{2} \frac{D+(s+s_2-c)}{2(s+s_2-c)}, $$ | (5.57) |
| $$ \sigma_{xp} = p \frac{1+I_{xp}}{2} \frac{D+(s+s_2-c)}{4(s+s_2-c)}. $$ | (5.58) |
В случае, если $l_2 < 8(s+s_2-c)$, при определении напряжений и коэффициента интенсификации вместо $(s+s_2)$ необходимо подставлять $s$ (толщиной накладного листа пренебрегают).
Напряжения на краю зоны накладного кольца определяются по формулам (5.49) и (5.55) при условии, что $I_p = 1$, $s_2 = 0$.
В общем случае все приложенные внешние нагрузки на штуцер можно разложить по трем направлениям, т.е. представить как одновременно действующие силы FR, FC, FL, и моменты MC, ML, MT. После определения напряжений от действующих сил и давления, суммарные напряжения в расчетных точках (1-8) определяются с учетом знаков согласно табл. 5.15.
При наличии коррозионно-активной сероводородсодержащей среды выполняется дополнительный расчет растягивающих напряжений на внутренних поверхностях обечайки (точки 2, 4, 6, 8):
| $$ \sigma_{in} = \max{\left\{ \frac{1}{2} \left( \sigma_{\theta}+\sigma_x+\sqrt{(\sigma_{\theta}-\sigma_x)^2+4\tau^2_{\theta x}} \right); 0 \right\}}. $$ | (5.59) |
| Таблица 5.15. Местные напряжения (с учетом знаков) обечайки в расчетных точках зоны врезки, нагруженной внутренним давлением и внешними нагрузками согласно WRC 107 | ||||||||
| Окружные напряжения, $\sigma_{\theta}$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Мембранные от $F_R$ | - | - | - | - | ||||
| Мембранные от $F_R$ | - | - | - | - | ||||
| Изгибные от $F_R$ | - | + | - | + | ||||
| Изгибные от $F_R$ | - | + | - | + | ||||
| Мембранные от $M_C$ | - | - | + | + | ||||
| Изгибные от $M_C$ | - | + | + | - | ||||
| Мембранные от $M_L$ | - | - | + | + | ||||
| Изгибные от $M_L$ | - | + | + | - | ||||
| Окружные напряжения от давления $\sigma_{\theta p}$ | + | + | + | + | + | + | + | + |
| Суммарные мембранные окружные напряжения $\sigma_{m\theta}$ | ||||||||
| Суммарные окружные напряжения $\sigma_{\theta}$ (форм. 5.3.1) | ||||||||
| Продольные напряжения, $\sigma_x$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Мембранные от $F_R$ | - | - | - | - | ||||
| Мембранные от $F_R$ | - | - | - | - | ||||
| Изгибные от $F_R$ | - | + | - | + | ||||
| Изгибные от $F_R$ | - | + | - | + | ||||
| Мембранные от $M_C$ | - | - | + | + | ||||
| Изгибные от $M_C$ | - | + | + | - | ||||
| Мембранные от $M_L$ | - | - | + | + | ||||
| Изгибные от $M_L$ | - | + | + | - | ||||
| Продольные напряжения от давления $\sigma_{xp}$ | + | + | + | + | + | + | + | + |
| Суммарные мембранные продольные напряжения $\sigma_{mx}$ | ||||||||
| Суммарные продольные напряжения $\sigma_{x}$ (форм. 5.3.1) | ||||||||
| Сдвиговые напряжения от $M_t$ | + | + | + | + | + | + | + | + |
| Сдвиговые напряжения от $F_C$ | + | + | - | - | ||||
| Сдвиговые напряжения от $F_L$ | - | - | + | + | ||||
| Суммарные сдвиговые напряжения $\tau_{\theta x}$ | ||||||||
| Приведенные общие напряжения $\sigma_{экв}$ | ||||||||
| Растягивающие напряжения на внутренней поверхности $\sigma_{in}$ | ||||||||

Штуцер-МКЭ 3.5. Руководство пользователя
Copyright © 2003-2025, НТП Трубопровод