

 |
Штуцер-МКЭ 3.5. Руководство пользователя |  |
Жесткость и податливость врезки в локальной системе координат определяется как для точки приложения усилий (на краю патрубка), так и для места врезки штуцера в каждом направлении. A также в глобальной системе координат для точки приложения усилий.
При определении жесткости врезки суммарные прибавки не учитываются.
Жесткость врезки определяется как отношение прикладываемых сил (моментов) к полученным соответствующим перемещениям (углам):
| $$ K_i = \frac{F_i}{u_i} $$ | (5.15) |
где $F_i$ - единичная сила заданная по i-ой степени свободы; $u_i$ - расчетное значение i-ой степени свободы на конце штуцера.
Если жесткости необходимо использовать совместно с балочной конечно-элементной моделью (например, в программном комплексе Старт-Проф [30]), в которой они моделируют некоторое оборудование (например, нестандартный тройник в Старт-Проф [30]), то необходимо включить опцию расчета жесткостей "Исключить балочную жесткость аппарата" (рис. 5.29).
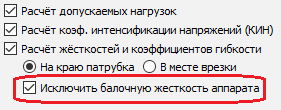 |
| Рис. 5.29. Включение\выключение возможности исключения балочной жесткости аппарата |
При исключении балочной жесткости программа дополнительно определяет перемещения конца штуцера\патрубка по балочной модели конструкции. Расчетные жесткости в этом случае определяются соотношениями:
| $$K_i = \frac{F_i}{u_i-u_{bi}}$$ | (5.16) |
где $u_{bi}$ - расчетное значение i-ой степени свободы на конце штуцера в балочной конечно-элементной модели.
Отметим, что для моделей с отводом (изгибом) исключение балочной жесткости не производиться.
Пример результатов расчета жесткости врезки приведен в таблице 5.6.
| Таблица 5.6. Жесткость врезки | ||||||
| Линейная, тс/мм | Угловая, тс·м/° | |||||
| KLx | KLy | KLz | KRx | KRy | KRz | |
| 59.1807 | 54.5664 | 67.9115 | 81.2115 | 761.1034 | 22.7687 | |
Значение податливостей врезки определяются как обратные величины жесткостей. В таблице 5.7 привед пример результатов расчета податливости врезки.
| Таблица 5.7. Податливость врезки | ||||||
| Линейная, мм/тс | Угловая, °/тс·м | |||||
| FLx | FLy | FLz | FRx | FRy | FRz | |
| 0.0169 | 0.0183 | 0.0147 | 0.0123 | 0.0013 | 0.0439 | |
Коэффициенты гибкости определяются для магистральной части тройников, отвода, а также врезок штуцеров и подпятника отвода при включенном флаге (рис. 5.29). Они используются, как правило, для передачи в другие программные комплексы, использующие балочную расчетную модель. С помощью коэффициентов гибкости вычисляются податливости врезки.
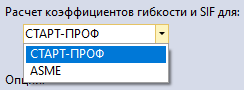 |
| Рис. 5.30. Задание расчетных формул коэффициентов гибкости |
При заданном расчетном документе ASME (рис. 5.30) коэффициенты гибкости вычисляются по следующим формулам:
| $$\begin{array}{lll} k_{a} & = & \sqrt[3]{ \lambda_a \frac{3 E I_b}{D^3} }, \\ k_{i} & = & \lambda_i \frac{E I_b}{D}, \\ k_{o} & = & \lambda_o \frac{E I_b}{D}, \\ k_{t} & = & \lambda_t \frac{E I_b}{D}, \\ \end{array} $$ | (5.17) |
где $k_a$, $\lambda_a$ - коэффициент гибкости и податливость от действия осевой силы на штуцер; $k_i$, $\lambda_i$ - коэффициент гибкости и податливость от действия изгибающего момента в плоскости аппарата и штуцера; $k_o$, $\lambda_o$ - коэффициент гибкости и податливость от действия изгибающего момента из плоскости аппарата и штуцера; $k_t$, $\lambda_t$ - коэффициент гибкости и податливость от действия крутящего момента на штуцер; $E$ - модуль продольной упругости; $I_b$ - момент инерции сечения штуцера; $D$ - наружный диаметр для ASME VIII Div. 1, 2 [9] и средний для ASME B31J [11].
Для остальных нормативных документов, в том числе и для программы Старт-Проф [30], коэффициенты гибкости определяются следующим образом:
| $$ \begin{array}{lll} k_{a} & = & \lambda_a E A, \\ k_{i} & = & \lambda_i \frac{E I_b}{D_o}, \\ k_{o} & = & \lambda_o \frac{E I_b}{D_o}, \\ k_{t} & = & \lambda_t \frac{G I_p}{D_o}, \\ \end{array} $$ | (5.18) |
где $A$ - площадь сечения штуцера; $I_b$ - момент инерции сечения штуцера; $I_p$ - полярный момент инерции сечения штуцера; $G$ - модуль сдвига материала штуцера; $D_o$ - наружный диаметр штуцера.
Для отвода коэффициенты гибкости вычисляются в соответствии с NB-3686.2 [8]:
| $$ \begin{array}{lll} k_{i} & = & \theta_i / \left(\frac{R}{E I_b}\int_0^\alpha{M(d\varphi)}\right), \\ k_{o} & = & \theta_o / \left(\frac{R}{E I_b}\int_0^\alpha{M(d\varphi)}\right), \\ k_{t} & = & \theta_t / \left(\frac{R}{G I_p}\int_0^\alpha{M(d\varphi)}\right). \\ \end{array} $$ | (5.19) |
где $\alpha$ - угол отвода; $\theta_i$ - расчетный угол поворота поперчного сечения в плоскости отвода; $\theta_o$ - расчетный угол поворота поперчного сечения из плоскости отвода; $\theta_t$ - расчетный угол поворота от действия крутящего момента.
Пример результатов расчета коэффициентов гибкости приведен в таблице 5.8.
| Таблица 5.8. Коэффициенты гибкости | ||
| Описание | Значения | |
| От осевой силы Fy | ka | 5.4614 |
| От изгибающего момента Mx (в плоскости) | ki | 4.0060 |
| От изгибающего момента Mz (из плоскости) | ko | 14.2885 |
| От крутящего момента My | kt | 0.3288 |

Штуцер-МКЭ 3.5. Руководство пользователя
Copyright © 2003-2025, НТП Трубопровод