Практика показывает, что при действии положительного температурного перепада и внутреннего давления в трубопроводе возникает продольное сжимающее усилие, в результате чего может происходить сильное выпучивание подземных участков труб, вплоть до выхода их на поверхность, поэтому необходимо производить проверку общей устойчивости прямых и криволинейных участков при бесканальной прокладке в грунте. Собственный вес грунта засыпки траншеи играет положительную роль в обеспечении устойчивости, поскольку удерживает трубу от выпучивания вверх.
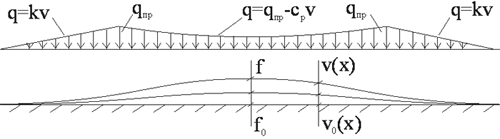
Рассмотрим заглубленный трубопровод с начальным искривлением (рис. 1) под действием эквивалентных сжимающих усилий S, вызванных температурным перепадом и внутренним давлением. Зависимость сопротивления грунта поперечным перемещениям принята в виде, показанном на рис. 2.

Рис. 1
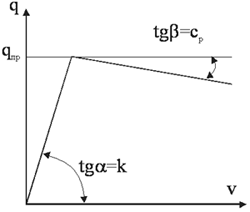
Рис. 2
Все вычисления выполняются по методике А.Б. Айнбиндера, описанной в [1]. При этом используется ряд допущений и гипотез, которые в основном идут в запас устойчивости.
Используется приближенный энергетический метод, основанный на анализе полной энергии системы, поэтому решение существенно зависит от принятых форм выпучивания.
Считается, что начальная форма прогиба совпадает с формой выпучивания.
Принимается, что при выпучивании трубопровода в вертикальной плоскости форма изгиба соответствует бесконечной жесткости основания под трубой. Для этого случая формы выпучивания приняты в виде:
начальный прогиб - 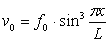 , дополнительный
прогиб -
, дополнительный
прогиб - 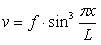 .
.
При выпучивании трубопровода в горизонтальной плоскости считается, что жесткость основания одинакова с обеих сторон трубопровода. Для этого случая формы выпучивания приняты в виде:
начальный прогиб - 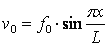 , дополнительный
прогиб -
, дополнительный
прогиб - 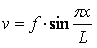 .
.
Такая расчетная модель применима при достаточно небольшом угле поворота трассы (острый угол α между прилегающими к кривой прямолинейными участками) – до 10 градусов.
При вычислениях пренебрегается влиянием упругой работы грунта на критическое продольное усилие. Считается, что по всей длине выпучивания грунт работает в пластической стадии, которая характеризуется предельным сопротивлением грунта поперечным перемещениям qпр и коэффициентом разгрузки Cр. Поэтому введены дополнительные проверки устойчивости в предположении упругой работы грунта.
Если плоскость начального изгиба трубопровода находится под произвольным углом к горизонту, то начальное искривление приводится независимо к вертикальной и горизонтальной плоскостям. В СТАРТ-ПРОФ для этого задается угол наклона к горизонту φ (угол между плоскостью кривой и плоскостью, проходящей через хорду кривой и перпендикулярную вертикальной плоскости).
Проверка устойчивости производится по 4-м условиям:
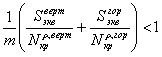 ; ; |
(1) |
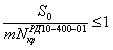 ; ; |
(2) |
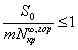 ; ; |
(3) |
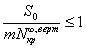 . . |
(4) |
где m – коэффициент условий работы (для при расчетах по РД 10-400-01 принимается равным 0.9, при расчетах по СНиП 2.05.06-85 зависит от категории трубопровода);
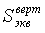 ,
,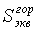 - эквивалентные усилия с учетом «самокомпенсации» за счет криволинейной
формы оси, вычисленные независимо в вертикальной и горизонтальной плоскости;
- эквивалентные усилия с учетом «самокомпенсации» за счет криволинейной
формы оси, вычисленные независимо в вертикальной и горизонтальной плоскости;
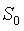 - эквивалентное усилие без учета «самокомпенсации» за счет криволинейной
формы оси;
- эквивалентное усилие без учета «самокомпенсации» за счет криволинейной
формы оси;
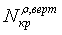 ,
,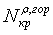 - критические усилия, вычисленные с учетом начального искривления трубопровода
и нелинейной зависимости сопротивления грунта поперечным перемещениям
в горизонтальной и вертикальной плоскостях;
- критические усилия, вычисленные с учетом начального искривления трубопровода
и нелинейной зависимости сопротивления грунта поперечным перемещениям
в горизонтальной и вертикальной плоскостях;
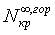 ,
,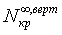 - критические усилия, вычисленные как для прямолинейного сжатого стержня
в линейно-упругой среде.
- критические усилия, вычисленные как для прямолинейного сжатого стержня
в линейно-упругой среде.
При вычислении 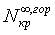 считается,
что жесткость грунта одинакова с обеих сторон, а при вычислении
считается,
что жесткость грунта одинакова с обеих сторон, а при вычислении 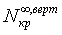 считается,
что жесткость грунта засыпки значительно меньше жесткости основания,
считается,
что жесткость грунта засыпки значительно меньше жесткости основания, 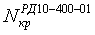 -
критическая сила, вычисленная по РД 10-400-01. Если угол поворота трассы
превышает 10 градусов то методика [1] не может быть использована и поэтому проверки
осуществляются только по последним 3-м условиям.
-
критическая сила, вычисленная по РД 10-400-01. Если угол поворота трассы
превышает 10 градусов то методика [1] не может быть использована и поэтому проверки
осуществляются только по последним 3-м условиям.
Если угол перелома превышает 10 градусов, проверка устойчивости криволинейного участка по формуле (1) не выполняется (поскольку методика не применима). В этом случае делается проверка только по формулам (2), (3) и (4).
1. Айнбиндер А.Б., Камерштейн А.Г. Расчет магистральных трубопроводов на прочность и устойчивость. М. “Недра”, 1982