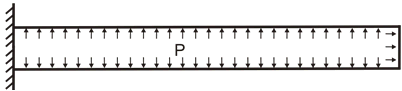
СТАРТ-ПРОФ автоматически учитывает следующие эффекты, связанные с наличием внутреннего давления в трубопроводе:
Учет распорных усилий и перемещений от неуравновешенного давления в СТАРТ
Учет распорных усилий и перемещений при наличии осевых компенсаторов
Удлинение незащемленной трубы от действия внутреннего давления состоит из двух частей. Первая часть вызвана воздействием давления на концевые заглушки (отводы, ройники и т.д.). Вторая часть вызвана укорочением труб по закону Гука.
Удлинение трубы от действия продольной силы:
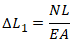
L – Длина трубы
E – Модуль упругости
Площадь поперечного сечения трубы
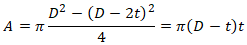
D – Наружный диаметр
t – Толщина стенки
N – Осевое внутренне усилие в трубе
Осевая сила равна силе от давления на заглушку
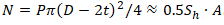
P – Внутреннее давление
Удлинение трубы равно
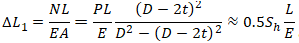
Sh – Кольцевое напряжение в трубе
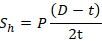
Согласно закону Гука осевая деформации трубы равна:
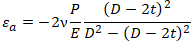
v – Коэффициент Пуассона
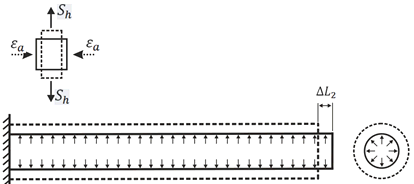
Укорочение трубы от внутреннего давления равно:
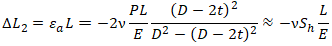
Полное удлинение трубы равно
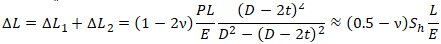
Если добавить удлинение от температурных расширений, то :
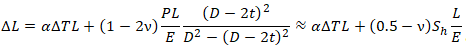
DT – Разность монтажной и рабочей температуры
a – Коэффициент температурного расширения
Осевое напряжение, вызванное внутренним давлением равно
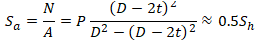
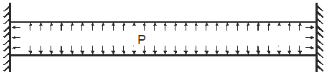
Для защемленной трубы между двумя мертвыми опорами удлинение равно нулю:
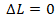
Удлинение трубы от осевой нагрузки R равно:
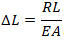
Следовательно, осевая нагрузка, необходимая, чтобы сжать трубу на величину DL равна:
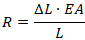
Если подставить вместо DL величину удлинения, полученную ранее, получим осевую нагрузку на опору, равную:
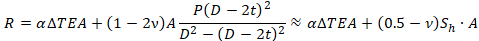
Величина внутреннего осевого усилия в трубе N может быт получено из условия равновесия около мертвой опоры. Осевая сила равна нагрузке на опору минус сила распора от давления, которая воспринимается непосредственно опорой:
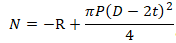
Окончательное уравнение осевого внутреннего усилия в защемленной трубе:
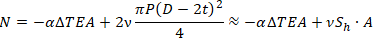
Осевое напряжение в защемленной трубе равно:
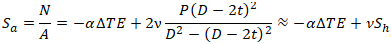
Если между одной из мертвых опор и защемленной трубой добавить упругую пружинку с жесткостью k, то труба будет являться частично защемленной. Если жесткость пружинки нулевая - получим незащемленную трубу. Если жесткость бесконечная - получим полностью защемленную трубу.
Пропустим вывод уравнений и приведем сразу окончательные выражения в таблице ниже. Значения "нагрузки на опору" так же можно назвать "эффективной продольная силой". Эффективная продольная сила равна истинной осевой силе за вычетом усилия распора от давления.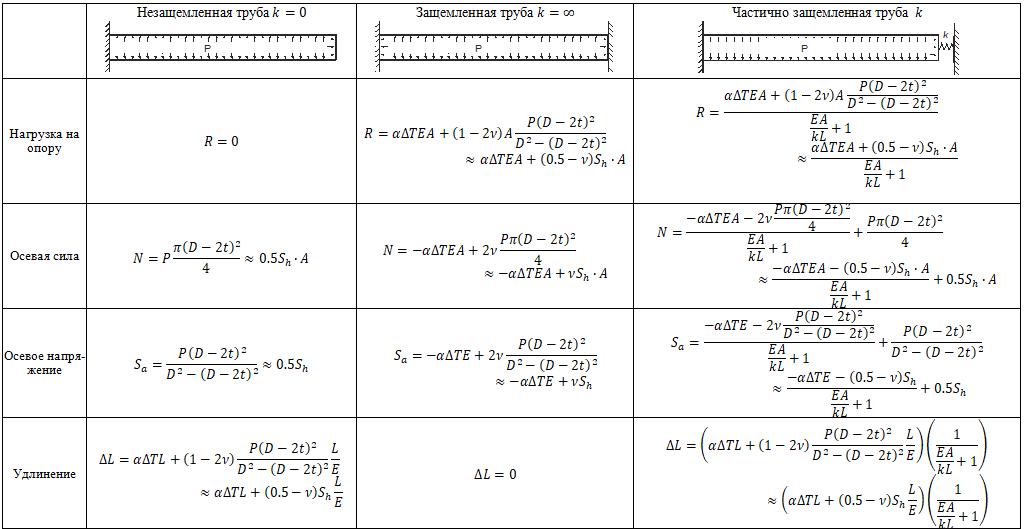
Истинная продольная сила используется для:
Вычисления осевых напряжений. См. таблицу напряжений
Проверки локальной устойчивости стенок (гофрообразования). См. таблицу устойчивости стенок
Эффективная продольная сила используется для:
В качестве нагрузок на опоры. См. таблицу нагрузок на опоры
В качестве нагрузок на штуцера оборудования (сосуды, аппараты, резервуары, насосы, компрессоры, турбины и т.д.). См. таблицу нагрузок на штуцера и оборудование
Для проверки фланцевых соединений на герметичность. См. таблицу Герметичность фланцевых соединений
Для проверки продольной устойчивости трубопровода. См. в СТАРТ-Элементы проверку устойчивости прямолинейных надземных, подземных и криволинейных трубопроводов.
Увидеть величину реальной и эффективной осевой силы можно в таблице "Внутренние усилия в участках" в локальных осях координат труб. Если галочка "Без учета распора от давления" не стоит, то мы видим истинную продольную силу в трубах. Если стоит, то видим эффективную продольную силу.
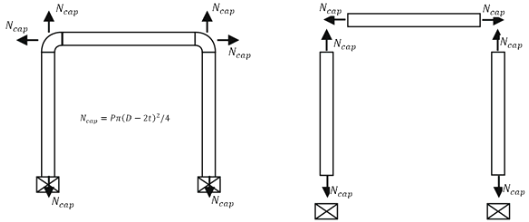
Почему именно эффективная осевая сила должна использоваться для проверки нагрузок на оборудования, а не истинная продольная сила в штуцере? Для этого следует мысленно поставить заглушку на трубе и штуцере оборудования:
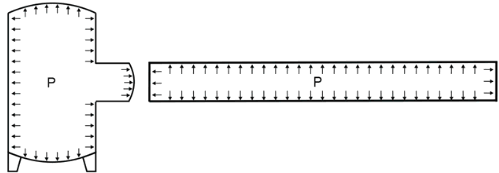
На самом деле, в местах присоединения трубопровода к оборудованию нет заглушки, поэтому распорного усилия нет. Однако, для сравнения с допускаемыми нагрузками следует использовать эффективную осевую силу, т.к. производители по методу конечных элементов определяют допускаемые внешние нагрузки для модели оборудования, находящегося под давлением с заглушкой на конце штуцера. То есть напряжения, вызванные растяжением штуцера от давления, действующего на заглушку уже учтены в расчете сосудов и аппаратов и определяются предельные значения внешних нагрузок без учета распора от давления. Следовательно, для проверки прочности штуцера следует использовать эффективную осевую силу, а не истинную. То же относится и ко всем другим видам оборудования (насосы, компрессоры и т.д.). В программе СТАРТ-ПРОФ в качестве нагрузок на все виды опор и оборудования выдаются эффективные осевые силы R, которые равны истинной осевой силе N за вычетом величины давления на заглушку
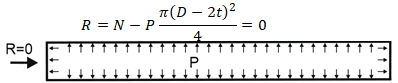
Точно такие же рассуждения применимы и для проверки герметичности фланцевых соединений. В формуле вычисления эффективного давления во фланцевом соединении уже есть составляющая от давления. Соответственно в качестве N мы должны прикладывать только дополнительные силы, вызванные другими нагрузками. Не давлением. То есть эффективную осевую силу.
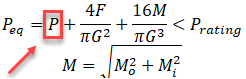
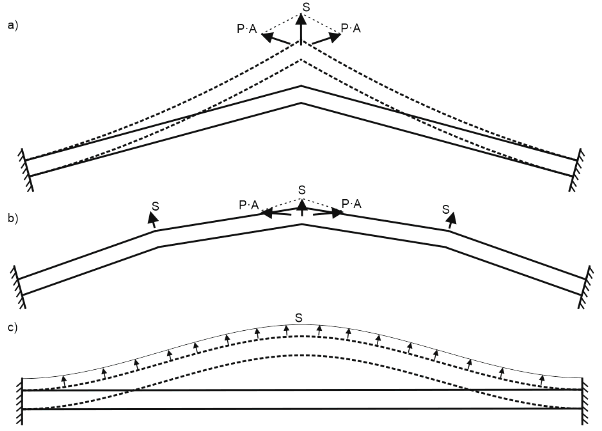
При расчете продольной устойчивости трубопровода мы должны использовать эффективную осевую силу. Дело в том, что одно только внутреннее избыточное давление способно вызвать потерю устойчивости трубопровода. Для того, чтобы объяснить этот феномен, представим себе деформированный вид трубопровода после потери устойчивости в виде ломаной, состоящей из двух труб (а). Силы распора от давления прикладываются к концам труб в узле излома и их равнодействующая создает поперечное усилие S, которое стремится вывести трубу из равновесия, толкает вбок.
Теперь представим, что весь деформированный трубопровода описан в виде ломаной (b). В этом случае "толкающих" сил S будет уже несколько - в каждой вершине. И, наконец, если деформированный вид трубы описан плавной линией, то "толкающие" силы S превратятся в распределенную нагрузку поперек оси трубы.
Пропустим вывод уравнений, укажем только, что для проверки продольной устойчивости должна быть использована именно эффективная осевая сила R и в случае действия одного только избыточного внутреннего давления она оказывается сжимающей:
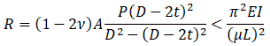
Также, этот феномен можно себе представить как потерю устойчивости воды внутри трубы. Вода (или другой продукт), сжата большой осевой силой (т.к. находится под давлением), и при потере устойчивости толкает трубу в поперечном направлении. То есть "воду" внутри трубы можно представить себе как сжатый стержень, теряющий устойчивость.
Во-первых, СТАРТ-Проф прикладывает растягивающие
распорные усилия от давления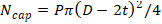 
по концам каждой
трубы
Во-вторых, помимо температурного расширения, СТАРТ-Проф учитывает дополнительное укорочение каждой трубы от внутреннего давления:
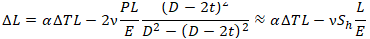
Комбинация этих двух эффектов и называется учетом распора от давления. Такая модель позволяет корректно моделировать любые виды трубопроводов: защемленные, незащемленные и частично защемленные.
Особенно важен учет распора от давления для:
В таких трубопроводах влияние распора от давления очень существенно и игнорировать его нельзя.
От внутреннего давления возникают неуравновешенные силы, действующие на заглушки и гофры сильфонных и линзовых компенсаторов (рис. 3, а), под действием этих сил незакрепленный трубопровод растягивается (рис. 3, б). Если трубопровод зажат между опорами, то не имея возможности растянуться, он передает распорные усилия на опоры (рис. 3, в).
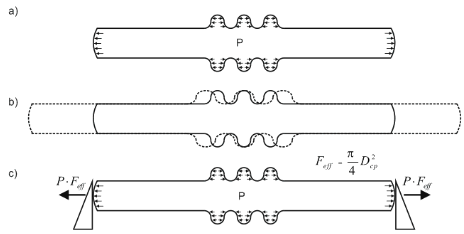
Рис. 3. Распорные усилия, передаваемые на опоры в трубопроводах с осевыми компенсаторами и без
Распорное усилие, передаваемое на опоры в прямой трубе ("давление на заглушку") равно (рис. 4, а):
P*Acap
Распорное усилие, передаваемое на опоры в осевом неразгруженном компенсаторе (рис. 4, б) равно
P*Aeff
Распорное усилие, передаваемое на опоры в осевом разгруженном компенсаторе (рис. 4, в) равно 0
Нагрузка от давления на оборудование складывается из давления на заглушку Acap и давления на "лишнюю" площадь гофр компенсатора (Aeff-Acap), таким образом, получается нагрузка Aeff.
Эффективные площади трубы и осевого компенсатора вычисляются по формулам на рис. 5.
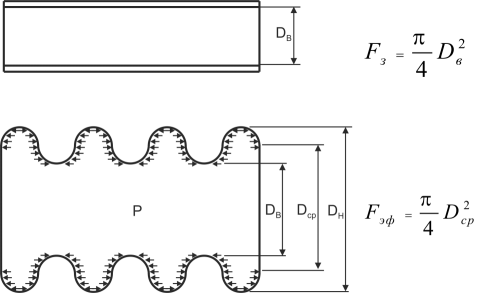
Рис. 5. Эффективные площади для трубы и осевого неразгруженного компенсатора
Расчетная модель осевого компенсатора в СТАРТ-ПРОФ показана на рис.
6. Давление в трубе уравновешивает часть распорного усилия в осевом неразгруженном
компенсаторе, поэтому при расчете, в узлах по обе стороны от осевого компенсатора
прикладываются нагрузки, равные разности распорных усилий в трубе и в
осевом компенсаторе. Давление на отводы будет равно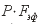 
.
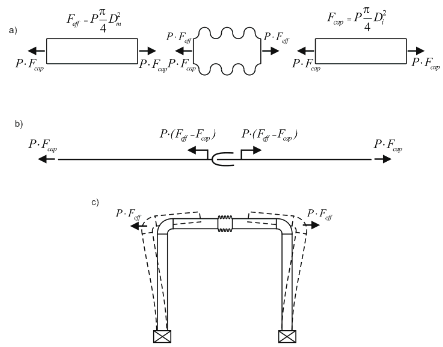
Рис. 6. Работа осевого неразгруженного компенсатора
Если эффективная площадь компенсатора задана равной 0, то нагрузка на отводы будет равна 0 (см. рис. 7).
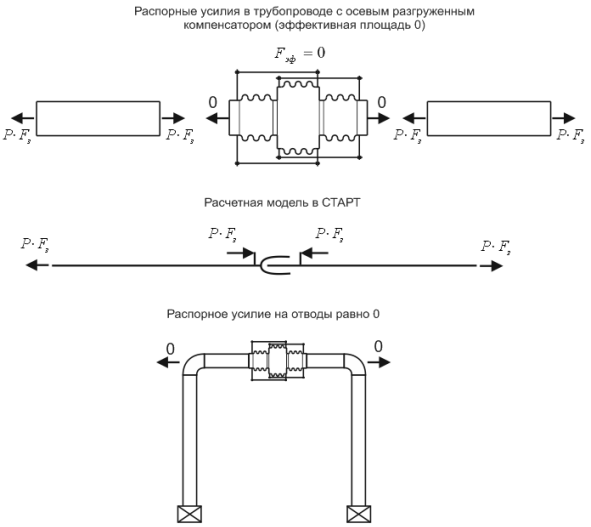
Рис. 7. Работа осевого разгруженного компенсатора
«Манометрический эффект» - это распрямление отвода, имеющего начальную овальность, под действием внутреннего давления (рис. 8). Этот эффект влияет на результирующие перемещения и нагрузки на опоры. Манометрический эффект проявляется только при величине коэффициента овальности a > 0.
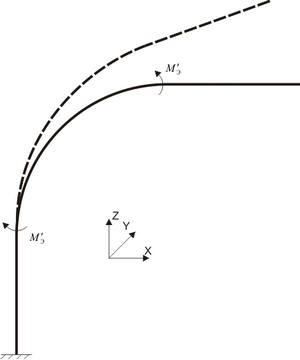
Рис. 8
Для моделирования манометрического эффекта к отводам автоматически прикладываются изгибающие моменты Mэ, действующие в плоскости отвода (рис. 3). Их величина вычисляется по формуле, полученной в соответствии с [2] и [3]:
,
где
a0 - коэффициент овализации, %
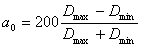
Кp - коэффициент податливости отвода,
Kэ - коэффициент, характеризующий влияние эллиптичности поперечного сечения на искривление оси отвода,
R - радиус оси отвода.
1. Айнбиндер А.Б. Расчет магистральных и промысловых трубопроводов на прочность и устойчивость. М. "Недра", 1991
2. Костовецкий Д.Л. Прочность трубопроводных систем энергетических установок. СПб.: "Энергия", 1973
3. Зверьков Б.В., Костовецкий Д.Л., Кац Ш.Н., Бояджи К.И. Расчет и конструирование трубопроводов. Справочное пособие. СПб.: "Машиностроение", 1979