

 |
Штуцер-МКЭ 3.5. Руководство пользователя |  |
Расчет жесткостей (податливостей) места соединения штуцера с сосудом (аппаратом) производится в трех направлениях:
| - | линейная жесткость вдоль оси штуцера (осевая), $K_R$; |
| - | угловая жесткость в поперечной плоскости обечайки, $K_{\theta}$; |
| - | угловая жесткость в продольной плоскости обечайки, $K_L$. |
Соответствующие указанным жесткостям податливости представляют собой обратные величины $\displaystyle\frac{1}{K_R}$, $\displaystyle\frac{1}{K_{\theta}}$ и $\displaystyle\frac{1}{K_L}$.
Связи штуцера с обечайкой в остальных трех направлениях принимаются абсолютно жесткими. Податливости в этом случае задаются равными нулю.
В случае, если конструкция врезки штуцера и обечайки не удовлетворяет условиям применения (например, наклонный штуцер) целесообразно применить метод конечных элементов.
Определение осевой жесткости врезки штуцера в цилиндрическую обечайку проводится с помощью зависимостей безразмерного параметра $\displaystyle\delta\frac{ER_m}{F_R}$ от геометрических характеристик деталей врезки $\displaystyle\left(\frac{R_m}{s}\right)$, $\displaystyle\left(\frac{C}{R_m}\right)$ и $\displaystyle\left(\frac{L_e}{R_m}\right)$ в соответствии с [18] (рис. 5.36).
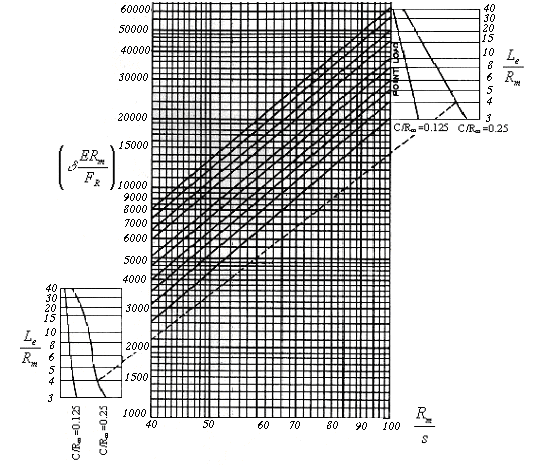 |
| Рис. 5.36. Относительное радиальное перемещение обечайки в зоне врезке штуцера |
При определении параметров используются следующие обозначения:
| $\delta$ | - | перемещение штуцера вдоль его оси; | $R_m = 0.5(D+s)$ | - | средний радиус цилиндрической обечайки без учета коррозии; | $L_e$ | - | эффективная длина цилиндрической обечайки. |
В случае смещения оси штуцера относительно центра обечайки на $l$:
| $$ L_e = L - 4\frac{l^2}{L}, $$ | (5.107) |
где $l = |0.5L-L_n|$ (рис. 5.37).
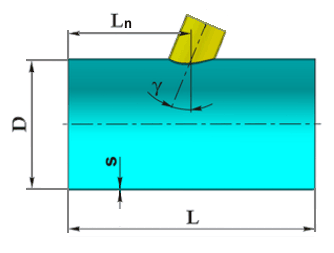 |
| Рис. 5.37. Расположение штуцера |
Осевая жесткость штуцера (радиальная обечайки) в месте врезки определяется как:
| $$ K_R = \frac{F_R}{\delta} = \frac{ER_m}{\displaystyle\delta\frac{ER_m}{F_R}}. $$ | (5.108) |
Для определения изгибной жесткости врезки штуцера в поперечной $K_{\theta}$ и продольной $K_L$ плоскостях обечайки используются зависимости безразмерных параметров $\displaystyle\frac{M_{\theta(L)}}{Es^3\varphi_{\theta(L)}}$ от геометрических характеристик деталей врезки $\displaystyle\lambda=\frac{d+2s_1}{2R_m}\sqrt{\frac{2R_m}{s}}$, $\displaystyle\Lambda=\frac{L_{eb}}{\sqrt{2R_ms}}$ и $\displaystyle\left(\frac{s}{s_1}\right)$, представленных на рис. 5.38 и 5.39.
| Здесь | $\displaystyle M_{\theta(L)}$ | - | изгибающий момент в поперечном ($\theta$) и продольном ($L$) направлениях обечайки соответственно; |
| $\displaystyle\varphi_{\theta(L)}$ | - | угол поворота штуцера от изгибающего момент в поперечном ($\theta$) и продольном ($L$) направлениях соответственно; | |
| $\displaystyle L_{eb} = \frac{2L^2-8L^2_e}{L+2\sqrt(0.25L^2-L^2_{\phi})}$ | - | эффективная длина обечайки для определения изгибной жесткости. |
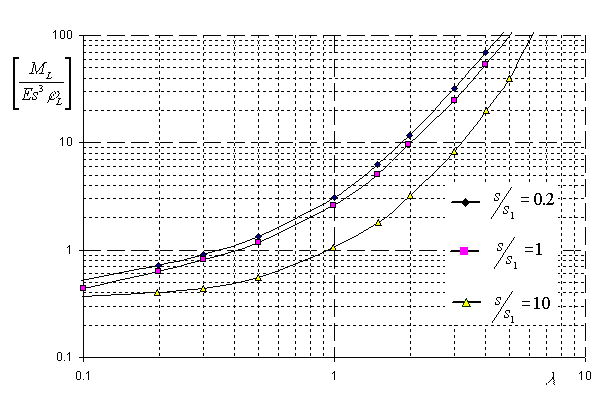 |
| Рис. 5.38. Относительное угловое перемещение в продольной плоскости при $\Lambda \ge 10$ |
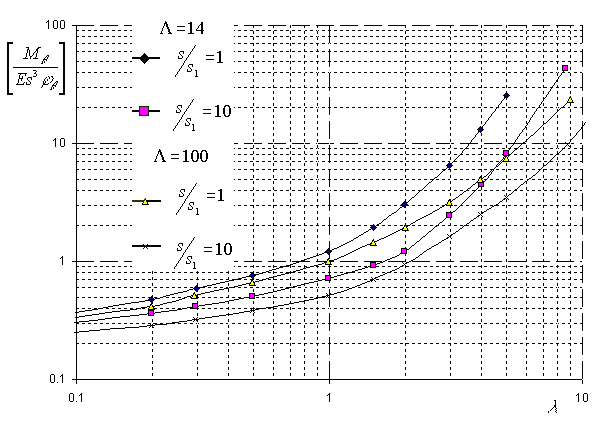 |
| Рис. 5.39. Относительное угловое перемещение в поперечной плоскости обечайки |
Изгибная жесткость в окружном и продольном направлениях:
| $$ K_{\theta(L)} = \frac{M_{\theta(L)}}{\varphi_{\theta(L)}} = Es^3\left(\frac{M_{\theta(L)}}{Es^3\varphi_{\theta(L)}}\right). $$ | (5.109) |
При наличии накладного кольца жесткость врезки штуцера зависит от его ширины $l_2$ и толщины $s_2$. При определении жесткости используется допущение, что перемещения штуцера под действием силовых факторов определяются как сумма перемещений штуцера диаметром $(d+2s_1)$, врезанного в обечайку с толщиной $(s+s_2)$, и перемещений штуцера с расчетным диаметром $(d+2s_1+2l_2)$ и обечайкой толщиной $s$ [15].
Жесткость (податливость) штуцера с укреплением отбортовкой определяется так же, как и для штуцера без укрепления. В то же время штуцер с укреплением вварной торовой вставкой или вварным кольцом рассчитывается как штуцер с укреплением накладным кольцом. В качестве ширины накладного листа используется ширина торовой вставки (вварного кольца). Вместо расчетной толщины $s_p = (s+s_2)$ принимается толщина торовой вставки (вварного кольца) $s^*$.
В случае использования проходящих штуцеров внутренние части при расчетах жесткости игнорируются.
Определение жесткости в месте врезки штуцера в сферическую обечайку вдоль оси штуцера производится с помощью зависимости безразмерного параметра $\displaystyle\left[\delta\frac{Es^2}{F_R R_m}\right]$ от геометрической характеристики деталей врезки $\displaystyle\left[u = 0.91\frac{d+s_1}{\sqrt{R_m s}}\right]$, представленной на рис. 5.40.
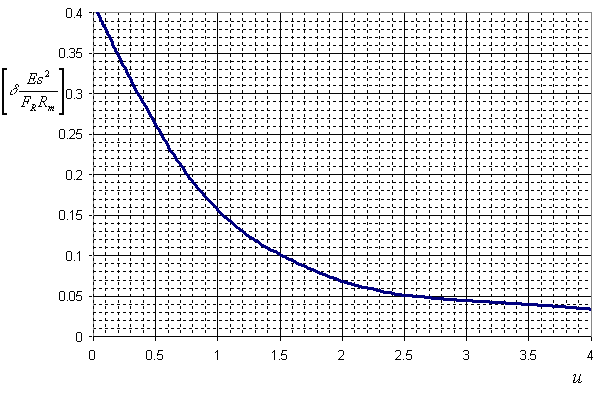 |
| Рис. 5.40. Относительное радиальное перемещение штуцера |
Расчетная схема врезки штуцера в сферическую обечайку, как и в случае прочностных расчетов, может также использоваться при определении жесткости соединения штуцера в эллиптическое днище.
Радиальная жесткость обечайки в месте врезки штуцера определяется как:
| $$ K_R = \frac{Es^2}{\displaystyle R_m\left[\delta\frac{Es^2}{F_R R_m}\right]}. $$ | (5.110) |
Для определения изгибной жесткости врезки штуцера в плоскости действия момента $M$ используется зависимость безразмерного параметра $\displaystyle\left[\frac{\delta}{M}\frac{Es^2}{\displaystyle\sqrt{\frac{R_m}{s}}}\right]$ от геометрической характеристики деталей врезки $\displaystyle\left[u = 0.91\frac{d+s_1}{\sqrt{R_m s}}\right]$, представленной на рис. 5.41.
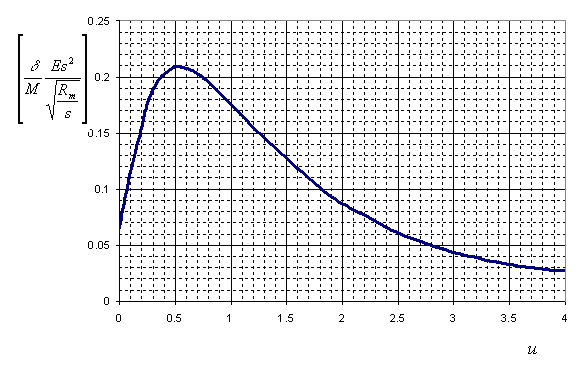 |
| Рис. 5.41. Относительное радиальное перемещение края штуцера |
По полученным перемещениям определяются угловые перемещения оси штуцера:
| $$ \varphi = \frac{2\delta}{d+s_1}. $$ | (5.111) |
Таким образом, изгибная жесткость врезки штуцера:
| $$ K_b = \frac{M}{\varphi} = \frac{d+s_1}{2}\frac{Es^2}{\displaystyle\sqrt{\frac{R_m}{s}}\left[\frac{\delta}{M}\frac{Es^2}{\displaystyle\sqrt{\frac{R_m}{s}}}\right]}. $$ | (5.112) |
При определении жесткости врезки штуцера при наличии накладного кольца, отбортовки, вварной торовой вставки или вварного кольца используются допущения, принятые для цилиндрической обечайки.

Штуцер-МКЭ 3.5. Руководство пользователя
Copyright © 2003-2025, НТП Трубопровод