Гибкая вставка

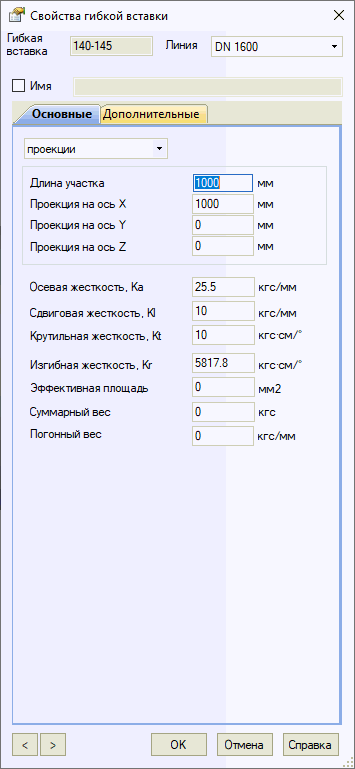
Параметр

Описание

Имя

Произвольный текст. Участки можно сортировать по названиям и выделять в дереве свойств участков и деталей

Проекции\сфера\цилиндр¹

Проекции - геометрия участка задается в виде длин проекций на глобальные оси координат D_X, D_Y, D_Z;
Cфера - геометрия участка задается в виде длины участка L и трех углов между осью участка и глобальными осями координат j_X, j_Y, j_Z;
Цилиндр - геометрия участка задается в виде длины проекции участка на плоскость XOY, проекции на ось Z и двух углов между проекцией участка на плоскость XOY и осями X и Y

Осевая жесткость, сдвиговая жесткость, крутильная жесткость, изгибная жесткость

Если задана сдвиговая жесткость, то изгибная жесткость вычисляется автоматически и наоборот по формулам:

KL=KR*3/L^2 и KR=KL*L^2/3,

где

KR - изгибная жесткость

KL - сдвиговая жесткость

Изгибную жесткость KR балочного компенсатора (двухузлового) следует задавать в четыре раза больше, чем для точечного компенсатора (одноузлового)

На рисунке ниже показаны модели двух видов компенсаторов: а - балочный (двухузловой) и б - точечный (одноузловой). Балочный элемент при изгибе может свободно перемещаться и образуется прогиб D, а точечный компенсатор не имеет возможности перемещаться при изгибе и прогиб D всегда нулевой. В таких моделях от одного и того же приложенного момента M угол поворота балки будет отличаться в 4 раза q2=4*q1,а следовательно и жесткости будут отличаться в четыре раза

KR балочного компенсатора = 4*KR точечного компенсатора

Следовательно, изгибные жесткости, приведенные в каталогах на компенсаторы нужно умножать на 4.

Эффективная площадь

Эффективная площадь для учета распорных усилий от давления. Для разгруженных компенсаторов и маталлорукавов в оплетке можно задавать 0

Суммарный вес

Суммарный вес всей гибкой вставки

Погонный вес

Погонный вес гибкой вставки