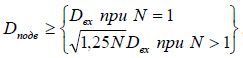
Расчет примыкающих трубопроводов

Выбор диаметров и проверка потерь давления на трубопроводах

После выбора клапана программа переходит к анализу подводящего и отводящего трубопроводов (в случае их задания). Прежде всего производится проверка внутренних диаметров трубопроводов. Согласно [1], пп. 8.1.2 и 8.2.1, для диаметра подводящего трубопровода Dподв должно выполняться соотношение:

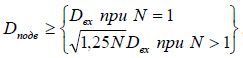
где Dвх - условный диаметр входного патрубка клапана. Если оно не выполняется, программа выводит соответствующее предупреждение.

Аналогично, для внутреннего диаметра (см. [1], п.8.2.2) отводящего трубопровода проверяется соотношение:

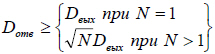
где Dвых - условный диаметр выходного патрубка клапана, и при необходимости выводится предупреждение.

Если диаметр подводящего трубопровода не задан, то программа принимает его равным Dвх при N =1 и наименьшим ≥ из стандартного ряда условных диаметров (2, 4, 6, 8, 10, 15, 20, 25, 32, 40, 50, 65, 80, 100, 125, 150, 200, 250, 300, 350, 400, 500, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000, 3000, 4000 – ряд условных диаметров, из которых осуществляется выбор, можно отредактировать в настройках программы) при N >1, о чем выводится соответствующее сообщение.

Аналогично если не задан диаметр отводящего трубопровода, он принимается наименьшим ≥ из стандартного ряда условных диаметров при N >1, и выводится соответствующее сообщение. Далее производится гидравлический расчет подводящего и отводящего трубопроводов и выполняется проверка допустимости величины падения давления на трубопроводах. Гидравлический расчет в соответствии с [1], п.8.2.1, проводится исходя из максимальной пропускной способности установленных клапанов, то есть для расхода Gmax = G(1+Kзап/100). Такой подход общепринят в мировой практике и обусловлен тем, что сама система аварийного сброса "не знает", какова рассчитанная проектировщиком требуемая пропускная способность, и работает в соответствии со своими фактическими характеристиками.

Расчет подводящего трубопровода проводится "по ходу потока", то есть исходя из избыточного давления P1 в начале трубопровода. Температура и газосодержание продукта принимаются равными T1 и х1. Падение давления на подводящем трубопроводе ΔPподв (точнее, его невозвратная часть - потери на трение и местные сопротивления -  без гидростатической и динамической части) согласно п.8.2.1 [1] не должно превышать 3% Pн. Программа проверяет это условие и выводит соответствующее сообщение, а также значение разности ΔPподв − 0,03Pуст (запас по давлению либо превышение). Кроме того, если диаметр подводящего трубопровода не был задан, а выбирался программой, в случае недопустимого падения давления программа последовательно увеличивает диаметр трубопровода, принимая следующий из ряда условных диаметров, и повторяет гидравлический расчет – до тех пор, пока падение давления не станет допустимым.

Заметим, что условие п.8.2.1 [1] - так называемое "правило 3%" - является инженерной рекомендацией, преследующей цель избежать неустойчивой работы клапана, при котором потери на подводящем трубопроводе могут вызвать постоянные циклы открытия и закрытия клапана большой амплитуды, с ударами золотника о седло (так называемый "chattering"), и привести к конечном счете к нарушению герметичности и даже разрушению седла. Данное правило было впервые предложено в середине XX века и с тех пор кочует в разных формулировках (3% от Pн, 1/3 от Pн-Pз и др.) из одного нормативного документа в другой. Современные исследования показывают, что данное правило не является ни необходимым, ни достаточным условием для предотвращения неустойчивой работы клапана. Более того, в некоторых случаях правило 3% вообще не может быть выполнено - например сопротивление самого входа в клапан или переключающего устройства может уже превышать 3%. Поэтому следование данному правилу является просто хорошей инженерной практикой, но ни в коем случае не является догмой и остается на усмотрение проектировщика. В настоящее время разрабатываются более точные инженерные методы расчета устойчивости работы систем аварийного сброса, которые, как ожидается, придут на смену "правилу 3%". В случае, если потери давления в подводящем трубопроводе превышают 3% Pн, следует провести проверку динамической устойчивости работы ПК в системе – экспериментально либо с помощью методов инженерного анализа, а также учитывать потери на подводящем трубопроводе при расчете пропускной способности ПК

Гидравлический расчет отводящего трубопровода проводится "против хода потока" - то есть исходя из заданного избыточного давления Pсбр в конце трубопровода. Температура продукта принимается равной T2. Величина падения давления на отводящем трубопроводе ΔPотв не должна превышать допустимого значения, которое в данной программе определяется исходя из 2-х критериев:

• Увеличение противодавления вследствие потерь давления на отводящем трубопроводе не должно вызывать закрытие клапана (точнее контакта золотника с седлом при его возвратно-поступательных движениях в ходе сброса – так называемый «chattering»);

• Увеличение противодавления вследствие потерь давления на отводящем трубопроводе не должно привести к падению расхода через клапан ниже заданного.

Различные норматично-методические документы расходятся в рекомендациях о пороговой величине потерь на отводящем трубопроводе, вызывающей закрытие несбалансированного предохранительного клапана - от величины overpressure (то есть P1-Pн) до 15% Pн. В данной программе в качестве данного критерия проверяется превышение динамического противодавления над давлением настройки клапана допустимых величин, значения которых регламентируется таблицей Б.1 ГОСТ 12.2.085-2017. Для сильфонных клапанов данное условие не проверяется.

Для второго критерия величина противодавления P2W , при котором расход через клапан точно равен W, при расчете по [1] определяется решением уравнения:

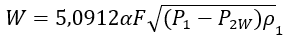- для жидких продуктов,

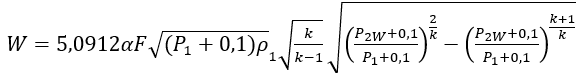- для газообразных продуктов.

При расчете методом HDI величина P2W аналогичным образом определяется с использованием уравнений метода HDI.

Поэтому программа определяет "максимальное" из обоих критериев противодавление для обычных клапанов и P2max = P2W для сильфонных клапанов, проверяет условие P2 = Pсбр + ΔPотв ≤ P2max и выводит соответствующее сообщение, а также величину разности P2max - P2 (величину запаса или превышения). Кроме того, если диаметр отводящего трубопровода не был задан, а выбирался программой, в случае недопустимого падения давления программа последовательно увеличивает диаметр трубопровода, принимая следующий из ряда условных диаметров, и повторяет гидравлический расчет – до тех пор, пока падение давления не станет допустимым.

Гидравлический и тепловой расчет трубопроводов

Гидравлический расчет подводящего и отводящего трубопроводов проводится по участкам. Участок - это прямой трубопровод или местное гидравлическое сопротивление.

Расчет трубопроводов при явном задании агрегатного состояния продукта (газ либо жидкость) в текущей версии проводится по модели изотермического течения. При задании неопределенного состояния продукта выполняется совместный тепловой и гидравлический расчет.

Подводящий трубопровод всегда рассчитывается "по потоку" (от начала к концу), в качестве параметров продукта в начале трубопровода принимаются давление полного открытия клапана и температура в защищаемой системе (для однокомпонентных продуктов на линии насыщения - заданное расчетное массовое газосодержание).

Отводящий трубопровод всегда рассчитывается "против потока" (от конца к началу), в качестве параметров продукта в конце трубопровода принимается заданное давление в системе сброса и температура или массовое газосодержание, рассчитанные на основе теплового баланса (с учетов эффекта Джоуля-Томпсона, но без учета теплообмена с окружающей средой).

При гидравлическом расчете прямого участка плотность и скорость газа определяются в зависимости от давления и температуры. Если плотность продукта на его концах отличается более чем на 1%, то участок разбивается на участки меньшей длины. Расчет потерь давления проводится при средних на участке плотности и скорости продукта. Учитывается изменение давления при подъеме или опуске трубопровода. Потери давления на трение определяются в зависимости от режима течения, шероховатости стенки трубы с учетом сварных швов [54]. Для расчета коэффициента гидравлического сопротивления  трения при турбулентном режиме используются уравнения, аппроксимирующие экспериментальные данные Мурина Г.А. [56] и Шевелева Ф.А. [57], а также формула Филоненко Г.К. [58] в зоне гладкого трения. В области ламинарного режима течения используется формула Гагена-Пуазейля [54]. Для кризисной области течения используются формулы Никурадзе и Самойленко [54]. Учет влияния сварных стыков труб проводился по методическим рекомендациям [54] с корректировкой по экспериментальным данным Шевелева Ф.А. [57]. Разработанный алгоритм обеспечивает расчет коэффициента гидравлического сопротивления трения с погрешностью не более 3%.

Расчет коэффициентов местных гидравлических сопротивлений проводится по формулам и уравнениям, аппроксимирующим экспериментальные данные, на основе справочника Идельчика И.Е. [54, 55]. Параметры местных сопротивлений могут быть заданы в исходных данных или приняты стандартными. Стандартными считаются: вход заподлицо со стенкой аппарата; плавный поворот с радиусом 1,5Dу (Dу - диаметр трубопровода) и углом поворота 90° (с радиусом 1,0Dу при Dу > 500); полностью открытые задвижки, клапаны, вентили и краны; диафрагмы с диаметром отверстия, равным 0,5Dу; тройники с углом отвода 90° и др.

При расчете трубопроводов, примыкающих к блоку (или нескольким блокам) предохранительных клапанов с переключающими устройствами, программа автоматически учитывает гидравлическое сопротивление переключающих устройств (ПУ). Последние автоматически вставляются в конце подводящего и в начале отводящего трубопровода как сопротивления с заданным коэффициентом сопротивления. Для одного блока и трубопровода с внутренним диаметром, равным номинальному проходу (условному диаметру) ПУ, в качестве коэффициента сопротивления принимается значение, указанное изготовителем ПУ и записанное в БД клапанов. В случае же выбора нескольких блоков и/или диаметра трубопровода, отличного от диаметра ПУ, программа рассчитывает и принимает эквивалентный коэффициент сопротивления, соответствующий правильной величине гидравлических потерь на ПУ в условиях квадратичного турбулентного режима течения, по формуле , где - коэффициент гидравлического сопротивления ПУ, DПУ - номинальный проход (условный диаметр) ПУ, Dтр - внутренний диаметр трубопровода, N - количество блоков.

Тепловой расчет проводится одновременно с гидравлическим расчетом на каждом участке. Температура продукта при расчете течения жидкости или газа определяется по уравнению Шухова, с дополнительным учетом тепла внутреннего трения и изменения плотности продукта при изменении температуры. Для газов при расширении дополнительно учитывается эффект Джоуля-Томсона. Учитывается наличие тепловой изоляции и покровного слоя, которые выбираются из базы данных материалов изоляции. При расчете изменения температуры в отводах и переходах их заменяют равными по длине участками прямой трубы. Арматура заменяется эквивалентными участками труб, которые для задвижек и вентилей составляют от 2 до 9 м. Потери тепла через опоры учитываются коэффициентом к общей длине трубопровода. Для подземных трубопроводов учитывается сопротивление грунта

Методика расчета двухфазного течения

При расчете двухфазных газожидкостных потоков в версии 3.х течение считается установившимся, а фазы – находящимися в состоянии термодинамического равновесия и имеющими одинаковые температуру и давление. При этом может учитываться "проскальзывание" жидкой и газовой фаз, то есть движение их с разными скоростями. Расчет выполняется совместно с тепловым расчетом и с расчетом массообмена (то есть с учетом испарения и конденсации продукта по ходу течения). Для выполнения данного расчета требуется расчет фазового равновесия, поэтому расчет возможен лишь при задании продукта с использованием библиотек СТАРС, WaterSteamPro или Simulis Thermodynamics.

В процессе расчета двухфазного газожидкостного потока для всех участков производится расчет:

• режима двухфазного течения в различных точках трубопровода;

• истинного объемного газосодержания (и на его основе расчет истинных скоростей фаз, а также гидростатических потерь на участках с перепадом высот);

• потерь на трение;

• потерь на местных сопротивлениях;

• потерь на ускорение потока;

• величины числа Маха.

Расчет ветвей производится методом прямого просчета ("по потоку" либо "против потока"), с разбиением при необходимости длинных прямых участков на части с малым изменением расчетных величин ([37], стр. 22-23).

Расчет изменения температуры потока и содержания фаз для течения с массообменном между фазами выполняется на основе уравнения баланса полной энергии. Рассчитывается изменение энтальпии продукта, и по энтальпии и давлению решается задача фазового равновесия, определяется температура продукта, содержание и составы фаз.

Если в защищаемой системе задается значение массового расходного газосодержания, большее нуля, но меньшее единицы, оно имеет приоритет над заданной температурой. В этом случае программа также решает задачу фазового равновесия, находит по максимальному давлению в защищаемой системе (давлению полного открытия клапана) и массовому расходному газосодержанию температуру продукта и составы фаз, и принимает их как условия в начале подводящего трубопровода.

В процессе расчета определяются точки полного перехода продукта в жидкое или газообразное состояние. Для подводящего трубопровода в этом случае программа автоматически переключается на расчет по методикам однофазного течения. Аналогичным образом отслеживается и обратный переход – начало вскипания или конденсации продукта – с автоматическим переключением программы на методики расчета двухфазного течения. Для отводящего трубопровода такое переключение в текущей версии не реализовано, выдается соответствующая диагностика и расчет прекращается.

Для определения режимов течения и выполнения расчета могут использоваться различные методики. Поскольку методы расчет двухфазных потоков в настоящее время интенсивно развиваются, и на сегодняшний момент не существует какого-то универсального общепризнанного подхода, в программе для наиболее важных решаемых задач реализована не одна, а целый набор методик, из которых можно выбрать наиболее подходящие для конкретной ситуации в соответствии с потребностями пользователя. При этом предусмотрена возможность достаточно гибко управлять тем, какие именно методики использовать для различных типов участков в различных случаях, с помощью специальных правил выбора методов двухфазного расчета. Пользователь может использовать собственные правила или воспользоваться одними из уже настроенных, входящих в состав поставляемой программы.

Определение режима двухфазного течения выполняется по наиболее популярным в последнее время так называемым "механистическим" моделям, основанным на моделировании физических механизмов смены режима течения. Программа различает и определяет 6 режимов течения: расслоенный гладкий, расслоенный волновой, прерывистый (перемежающийся), пузырьковый, дисперсно-пузырковый, кольцевой. В настоящее время программа не различает различные разновидности данных режимов, например разновидности прерывистого течения (такие как снарядное, пробковое и вспененное) или кольцевого течения (дисперсно-кольцевое, волновое кольцевое или клочковато-кольцевое), такую возможность планируется добавить в будущем.

Рассчитанные режимы течения можно использовать для более адекватного выбора методик расчета истинного объемного газосодержания и потерь давления. В дальнейшем планируется добавить в программу специализированные расчетные методики этих величин на основе моделей тех или иных режимов течения.

Для расчета истинного объемного газосодержания в программе реализован целый ряд типов корреляций: HEM (однородная равновесная модель течения), корреляции степенного типа, корреляции на основе потока дрейфа и наиболее популярные эмпирические корреляции. Корреляции степенного типа в настоящее время представляют скорее исторический интерес и реализованы для совместимости с другими программами. Для больших и средних скоростей потока можно рекомендовать использовать корреляцию Premoli, а при небольших скоростях – подходящие по углу наклона потока корреляции Rouhani, Dix-Ghajar-Woldesemayat или Goda-Hibiki-Kim-Ishii-Uhle. Сравнительный обзор применимости и точности различных методик можно найти в [79].

Рассчитанное истинное объемное газосодержание используется при расчете потерь на перепадах высот, а также некоторых выводимых величин (истинных скоростей фаз и др.)

Для расчета потерь на трение газожидкостного потока в версии 3.50 программы реализованы два типа корреляций – на основе модели однородного течения и с использованием двухфазных мультипликаторов.

Первая группа методик рассчитывает потери на трение как для однофазного потока с теплофизическими свойствами газожидкостной смеси. Двухфазность течения при этом учитываются при расчете вязкости смеси (в методике Beattie – Whalley) или числа Рейнольдса смеси (в методике Shannak).

Во второй группе методик рассчитываются потери на трение для однофазного течения (для жидкой или газовой фазы) с последующей корректировкой на множители, учитывающие газосодержание и свойства фаз. При реализации в программе методик Friedel и MSH их возможности несколько расширены по сравнению с авторскими вариантами путем применения для расчета коэффициента гидравлического трения формулы Черчилля (как это рекомендуется в [71]), что позволяет применять их на всем диапазоне значений числа Рейнольдса, а также учесть влияние шероховатости стенок труб. Также приводятся рекомендации по применению методик двухфазных мультипликаторов, предложенные Whalley [34, 60]. Более детальные рекомендации также предложены в [85].

Вопрос расчета потерь давления на местных сопротивлениях для газо-жидкостного течения до сих пор современными исследователями изучен недостаточно. В текущей версии программы реализованы основные предложенные для этого случая в литературе методы расчета, преставляющие собой разновидности метода двухфазных мультипликаторов для местных сопротивлений. Рекомендации по применению данных методов для различных видов местных сопротивлений даны в [34, 71, 88]. Для типов местных сопротивлений, для которых рекомендации отсутствуют, применяется методика HEM.

Потери на ускорение потока рассчитываются с использованием модели HEM в соответствии с рекомендацией [59] для адиабатического течения.

Расчет средней вязкости газожидкостной смеси выполняется по методике Beattie – Whalley [81].

В поставляемом в составе дистрибутива программы файле настроек выбора методов расчета двухфазного течения HST.xml выбраны следующие методы расчета, имеющие широкую сферу применения:

• расчет режима течения по методике Barnea;

• расчет истинного газосодержания по методике Premoli;

• расчет потерь на трение методами двухфазных мультипликаторов согласно рекомендациям Whalley;

• расчет потерь на местных сопротивлениях согласно рекомендациям [88].

При расчете двухфазного, а также течения газообразного продукта в отводящем трубопроводе (при заданном "неопределенном" состоянии продукта) программа определяет и корректно рассчитывает места критического истечения (в конце прямых участков, на выходе из прямой трубы, в диффузорах и внезапных расширениях), в которых число Маха равно 1, нарушается сплошность потока и имеет место скачок уплотнения. В этих местах программа последовательными итерациями на основе уравнений материального и энергетического баланса определяется параметры продукта перед скачком уплотнения. Для расчета прямых участков, где число Маха близко к единице и имеет место очень быстрое изменение давления, температуры и других параметров продукта по длине, применяется специальный алгоритм расчета. Течение описывается системой обыкновенных дифференциальных уравнений по давлению, которые решаются с использованием методов Рунге-Кутты и квадратурных формул (подробнее см. [89]). Для расчета внезапных расширений при докритическом течении газа в этом случае используется подход, представляющий собой обобщение уравнений Борда-Карно на основе работ [96, 97, 98]. Для расчета диффузоров при докритическом течении газа используется подход, предложенный в [95].